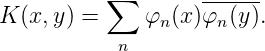
Keywords: Uniform distribution of sequences, Interpolation, Numerical Integration, Hilbert Space, Reproducing Kernel, Eigentheory of sequences.
Grundlage der folgenden Untersuchungen sind Hilberträume mit reproduzierendem
Kern, wie sie in der klassischen Arbeit von Aronszajn [1] und bei Meschkowski [2]
dargestellt sind.
Sei E≠∅ und K(⋅,⋅) : E ×E → ℂ ein positiv definiter Kern: Für alle a1,…,aN ∈ ℂ und t1,…,tN ∈ E sei also ∑ n=1N ∑ m=1Na namK(tm,tn) ≥ 0.Dann erzeugt K(⋅,⋅) einen Hilbertraum von Funktionen f(⋅) : E → ℂ, der durch K(⋅,⋅) reproduziert wird, wobei f(⋅) → f(x) stetig sind. Gelegentlich werden wir voraussetzen, dass E eine Metrik d(⋅,⋅) trägt und (E,d) kompakt ist. Wir setzen voraus, dass der Kern K(⋅,⋅) strikt positiv definit ist: aus ti≠tk,i≠k,i,k = 1,…,N und ∑ i=1N ∑ k=1Na kaiK(ti,tk) ≥ 0 folgt a1 = a2 = … = aN = 0. Gleichbedeutend sind die Aussagen: je endlich viele K(t,t1),…,K(t,tN),ti≠tk, sind linear unabhängig bzw. die Funktionen f(x) ∈ H trennen die Punkte von E. Wir führen nun in E die Metrik dK ein:
Definition. dK(x,y) = ||K(t,x) - K(t,y)||.
Zu zeigen ist nur, dass aus dK(x,y) = 0 folgt x = y: angenommen es gibt x,y,x≠y, sodass dK(x,y) = 0. Dann ist K(t,x) = K(t,y). Daraus folgt f(x) =< f(⋅),K(⋅,x) >=< f(⋅),K(⋅,y) > für f(⋅) ∈ H. f(x) = f(y) für alle f ∈ H bedeutet aber, dass H nicht die Punkte trennt, was unserer Voraussetzung widerspricht. Wir setzen nun weiters voraus, dass (E,dK(⋅,⋅)) kompakt ist. Trägt nun E eine weitere Metrik d(⋅,⋅)), die (E,d) zu einem kompakten Raum macht und die mit der Topologie von (E,dK) vergleichbar ist, so stimmen die beiden Topologien überein, da ein kompakter T2- Raum ein gröbster Hausdroffraum und ein feinster kompakter Raum ist. Hinreichend unter unseren Kompaktheitsvoraussetzungen ist z.B., dass die Abbildung x → K(⋅,x) von (E,d) → H stetig ist. Dann sind bereits die Räume (E,d) und ({K(⋅,x),x ∈ E},dK) homöomorph. Ist nun in einem allgemeinen (E,K,H) eine Orthonormalbasis (φn(x))n gegeben, so gilt
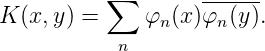
Definition. (xn)n,xn ∈ E, heißt total, wenn K(⋅,xn),n = 1, 2,…, in H total ist.
(xn)n ist also genau dann total, wenn aus f(xn) =< f(⋅),K(⋅,xn) > = 0 folgt
f = 0.
Sei nun x1,…,xN ∈ E,xi≠xk,i≠k.HN := span{K(x,xi),…,K(x,xk)}.
Wir wenden das Schmidt-sche Orthogonalisierungsverfahren auf K(x,x1),…,K(x,xN) an und erhalten eine ONB für HN : τ1(x),τ2(x),…τN(x).
Der Kern KN(x,y) = ∑
n=1Nτ
n(x)τn(y) reproduziert HN, wogegen
KN⊥(x,y) = K(x,y) - K
N(x,y) den Orthogonalraum HN⊥ reproduziert.
Da weiters für n ≤ m τm+1(x) ⊥ τnx gilt, ist τm+1(x) ⊥ Hm, also
< τm+1(x),K(x,xn) >= τm+1(xn) = 0. Also gilt τm(xn) = 0 für m > n. Ebenso
gilt τn(xn) > 0 gemäß dem Orthogonalisierungsverfahren. Sei GN die Gramsche
Matrix GN = (< K(x,xm),K(x,xn) >)m,n=1N = (K(x
n,xm))m,n=1N. G
N ist
nichtsingulär und positiv definit. Aus der Darstellung KN = K - KN folgt
unmittelbar KN⊥(x,x
n) = 0 für n = 1,…,N. Man sieht wegen
KN(x,y) = ∑
n=1Nτ
n(x)τn(y)
GN = (KN(xn,xm))m,n=1N = (K(x n,xm))m,n=1N und
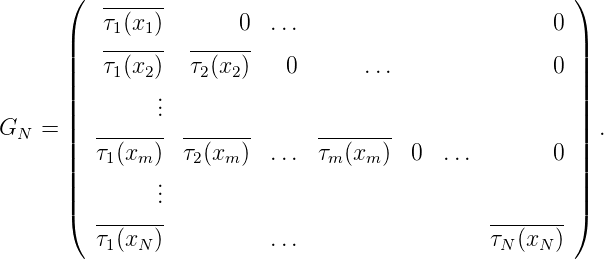
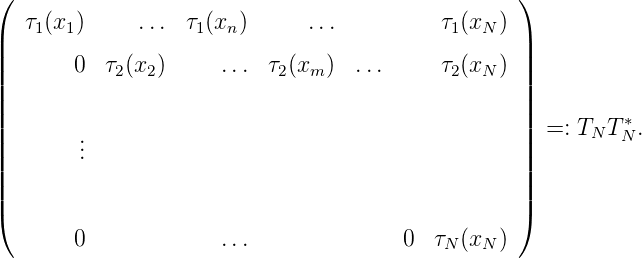
Die Darstellung GN = TNTN* ist die Cholesky-Zerlegung von G N.
Es folgt sofort
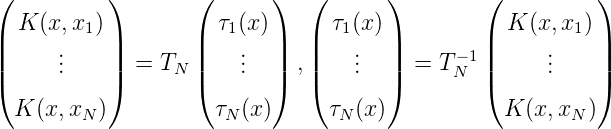
Für die zu K(x,x1),…,K(x,xN) duale Basis von HN, bezeichnet mit
l1(x),…,lN(x), gilt < K(x,xn),lm(x) >= δnm. l1(x),…,lN(x) besitzen die
Darstellung
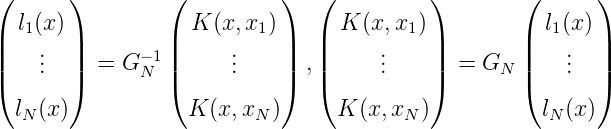
Es gilt Gram (l1(x),…,lN(x)) = (< lm(x),ln(x) >)m⋅n=1N = G N-1.
Wegen < lm(x),K(x,xn) >= lm(xn) = δmn gilt für
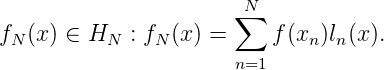
Insbesondere gilt
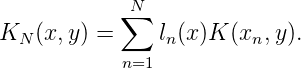
Die Cholesky-Zerlegung der positiv definiten Matrix GN-1 sei
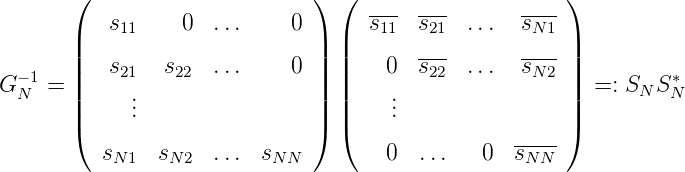
Ebenso, wie TN-1 die Basis K(x,x 1),…K(x,xN) von HN zu τ1(x),…,τN(x) orthogonalisiert, orthogonalisiert SN-1 die duale Basis l 1(x),…,lN(x) zu einer ONB σ1(x),…,σN(x) :
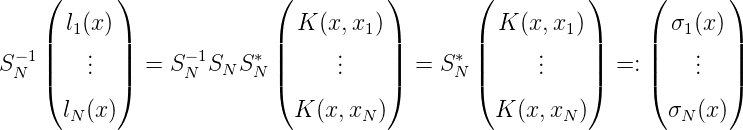
Durch Einsetzen x = x1,x2,…,xN, und weil SN-1 eine untere Dreiecksmatrix ist, erhält man sofort
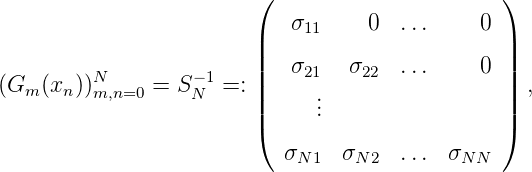
also σm(xn) = 0 für n > m, dual zu τm(xn) = 0 für n < m. Sei WN = SN*T N, dann ist WN unitär:
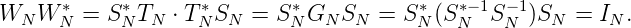
Demgemäß gilt
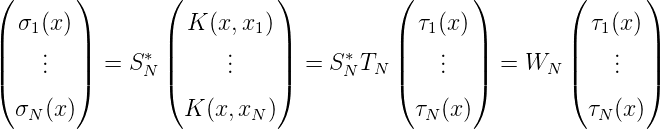
Es folgt weiters
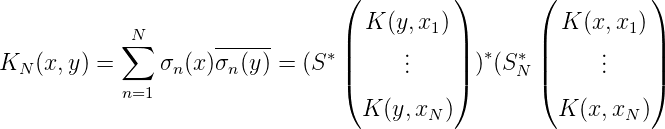
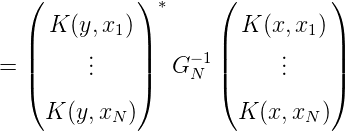
Die Diagonalisierung von GN mittels der unitären Matrix UN führt zu einer weiteren ONB λ1(x),…,λN(x) von HN: Sei also
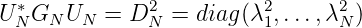
und
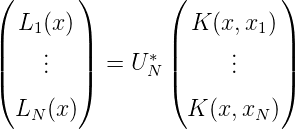
Direktes Nachrechnen zeigt Gram(L0(x),…,LN(x)) = (< Lm,Ln >)m,n=1N = (λ
mλnδmn)m,n=1N.
Also gilt Gram(L0(x),…,LN(x)) = DN2. Also sind die Funktionen λ n(x),n = 1,...,N, mit λn(x) = Ln(x)∕λn eine ONB für HN, wobei
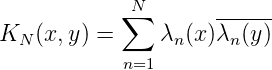
ist.
Da sich die Koeffizienten eines Vektors bei einer linearen Transformation kontragradient transformieren gilt wegen
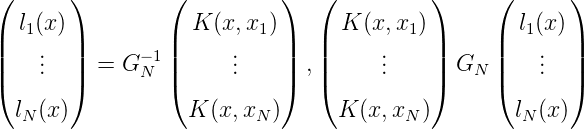
für fN(x) = f(x1)l1(x) + … + f(xN)lN(x) =: 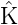 1K(x,x1) + ...+
1K(x,x1) + ...+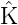 N(x,xN)
N(x,xN)
Analog gilt für fN(x) =  1τ1(x) + ... +
1τ1(x) + ... +  NτN(x),
NτN(x),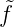 n =< fN,τn >,
n =< fN,τn >,
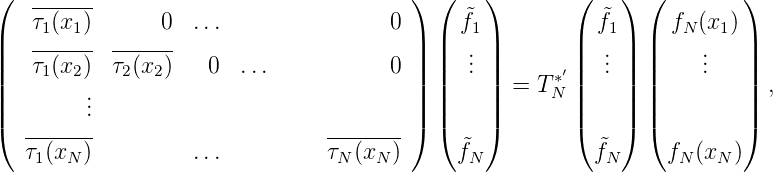
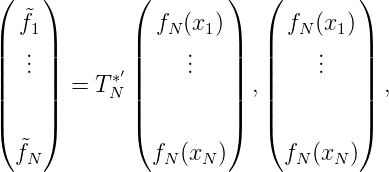
also
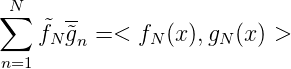
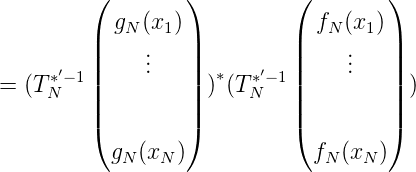
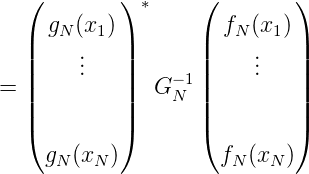
Sei nun (xn)n eine unendliche Folge in E. Wir nehmen ohne Beschränkung der Allgemeinheit an, dass xn≠xm für n≠m. Das Schmidtsche Orthogonalisierungsverfahren liefert eine orthonormale Folge τn(x) ∈ H,n = 1, 2,…, sowie eine Folge von Hilberträumen HN = span{K(x,x1),…,K(x,xN)}⊆ HN+1 mit Kernen
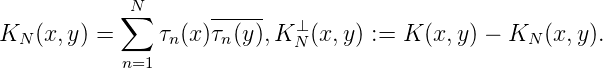
Offensichtlich gilt
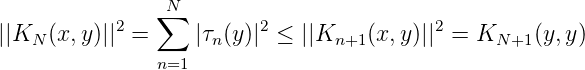
und
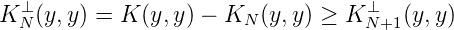
Es gilt der Satz:
Satz 1. (xn)n=1∞ ist total, genau wenn K(x,y) = ∑
n=1∞τ
n(x)τn(y). Sei
weiters fy(x) = K∞⊥(x,y) = K(x,y) - K
∞(x,y). K∞⊥(x,y)⊥K(x,x
n)
für n = 1, 2,... und y ∈ E : fy(xn) =< fy(x),K(x,x,n) >= 0. Da
(xn)n total ist, folgt fy(x) = 0 für jedes y, also K∞⊥ = 0. Damit ist
K(x,y) = ∑
n=1∞τ
n(x)τn(y) gezeigt. Sei nun umgekehrt f ∈ H so, dass
f(xn) = 0 für n = 1, 2,...,n dann gilt mit  m =< f(x),τm(x) > die
Entwicklung f(x) = ∑
m
m =< f(x),τm(x) > die
Entwicklung f(x) = ∑
m mτm(x) und f(xn) = ∑
m
mτm(x) und f(xn) = ∑
m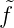 mτm(x) = 0. Für n = 1
folgt 0 = f(x1) =
mτm(x) = 0. Für n = 1
folgt 0 = f(x1) = 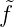 1τ1(x1), also
1τ1(x1), also 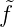 1 = 0. Ist bereits
1 = 0. Ist bereits 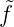 1 = ... =
1 = ... = 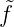 n = 0, so folgt
f(xn+1) = 0 =
n = 0, so folgt
f(xn+1) = 0 = 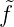 n+1τn+1(xn+1), also
n+1τn+1(xn+1), also 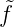 n+1 = 0. Was zu zeigen war.
n+1 = 0. Was zu zeigen war.
Das bedeutet, dass (xn)n=1∞, genau dann total ist, wenn für jedes y ∈ E
gilt
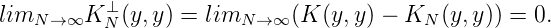
Definition. TN2(y) = K(y,y) - K N(y,y) = K(y,y) -∑ n+1N|τ n(y)|2 ist die N-te Totalität der Folge (xn)n an der Stelle y ∈ E.
Es gilt also der Satz
Satz 2. (xn)n ist genau dann total, wenn TN2(y) = ∑ n>N|τn(y)|2 ist. Genau dann gilt offenbar limN→∞TN2(y) = 0 für y ∈ E.
Unter unserer Voraussetzung der starken Kompaktheit von E in der übertragenen starken Topologie gilt der Satz
Beweis. Die Normen K(y,y)
12, K˙N(y,y)ˆ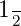 sind stetig und TN+1 < TN. Wenn (xn)n total ist folgt also
nach Dini, dass auch limN→∞max TN(y) = 0. Ist umgekehrt limN→∞TN = 0,
so ist limN→∞TN(y) = 0 f¨ur y ∈ E, also (xn)n total. __
sind stetig und TN+1 < TN. Wenn (xn)n total ist folgt also
nach Dini, dass auch limN→∞max TN(y) = 0. Ist umgekehrt limN→∞TN = 0,
so ist limN→∞TN(y) = 0 f¨ur y ∈ E, also (xn)n total. __
Bemerkung. Wenn (xn)n nicht total ist, reproduziert K∞(x,y) = ∑ n=1∞τ n(x)τn(x) den echten Teilraum H∞ ⊂ H und es gilt TN2(y) → T ∞2(y). Es ist K(x,y) = K∞(x,y) + K∞⊥(x,y) und T ∞2(y) = K ∞⊥(y,y) ≥ 0, wobei T∞(y) nach dem Satz von Dini stetig ist. Jedenfalls ist die Folge in H∞ total, was für numerische Prozesse in H∞ nützlich ist.
Eine Anwendung: Sei (xn)n total und f(x) ∈ H. Dann ist
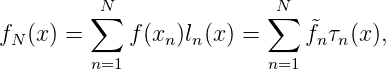
wobei die Funktionen l1(x),...,lN(x) von x1,...,xN abhängen.
Dann ist |f(x)-fN(x)| = | < f(t),K(t,x)-KN(t,x) > |≤||f||||K(t,x)-KN(t,x)|| = ||f||TN(x) ≤||f||TN.
Es gilt also der Satz:
Satz 4. Die Interpolationsfunktion fN(x),fN(xn) = f(xn),n = 1,...,N approximiert f(x) auf E gleichmäßig und es gilt |f - fN|≤||f||TN, wobei für totale (xn)n gilt limn→∞TN = 0.
Wir verwenden nun die aus der Theorie der Folgen in kompakten separablen Räumen bekannte Dispersion einer Folge x1,...,xN zur Abschätzung der Totalität TN von x1,...,xN. Ist (E,d) ein kompakter metrischer Raum, so wird die Größe
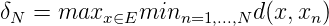
als Dispersion der Punktmenge {x1,...,xn} bezeichnet. δN ist eng verwandt mit der Hausdorff-Distanz der Menge {x1,..,xN} von der Grundmenge E. Es ist unmittelbar zu sehen, dass limN→∞δN = 0, genau wenn (xn)n dicht in E ist. Es gilt der Satz:
Beweis. K(t,x) = KN(t,x) + KN⊥(t,x), K N⊥(t,x n) = 0 für n = 1,...,N dK2(x,x n) = ||K(t,x)-K(t,xn)||2 = ||K N(t,x)-KN(t,xn)||2+||K N⊥(t,x)- KN⊥(x,x n)|| = ||KN(t,x) - KN(t,xN)||2 + || K N⊥(t,x)||2 __
Also ist für x ∈ E
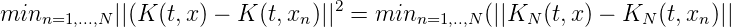
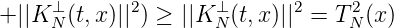
So gilt
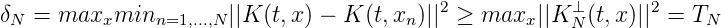
Eine Folgerung: Bei der Verwendung des Interpolationsoperators f(x) → fN(x) = ∑ n=1Nf(x n)ln(x) gilt
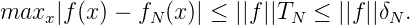
Wir geben nun zwei extreme Beispiele für Hilberträume mit reproduzierbarem Kern, um das mögliche Verhalten der Totalität und der Dispersion einer Folge zu beleuchten:
Beispiel 1. Sei E = D = {z : |z| ≤ 1}, 0 < |q| < 1. Wir betrachten den Kern K(z,w) = ∑ n=0∞(qz)n(qw)n = ∑ n=0∞φ n(z)φn(w) = 1∕(1 - qzqw).
K(z,w) ist stetig in D×D. K(z,w) ist strikt positiv definit: Sei a1,...,aN ∈ ℂ,t1,...,tN ∈D. Dann ist
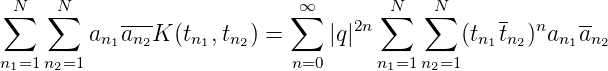
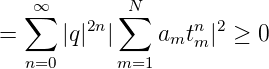
Zur strikten positiven Definitheit: Seien ti≠tk für i≠k, dann hat das lineare Gleichungssystem
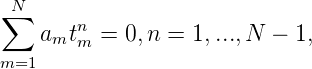
nur die triviale Lösung am = 0,m = 1,...,N, da die (Vandermond’sche) Determinante V N des Systems wegen ti≠tk,V n≠0 ist. Also ist K(z,w) in D strikt positiv definit. Weiters ist die Abbildung w → K(z,w) wegen des Identitätssatzes für Potenzreihen bijektiv. Der von K(z,w) auf E = D erzeugte Hilbertraum lautet
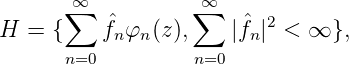
wobei φn(z)⊥φm(z) für n≠m, und 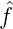 n =< f(z),φn(z) > ist. Sei f(z) ∈ H
und (zn)n eine beliebige Folge aus D, und sei f(zn) = 0,n = 1, 2,...
Da (zn)n in D einen Häufungspunkt hat, gilt nach dem Identitätssatz für
analytische Funktionen f(z) ≡ 0 im Analytizitätsbereich B ⊃ D. Also
ist jede unendliche Menge {zn}n ⊆ D in H total, TN → 0. Falls also
z.B. (zn)n in D konvergiert, ist (zn)n in D nirgends dicht. So kann die
Dispersion δN der Folge z1,...,zN beliebig schlecht gemacht werden. D und
{K(z,w),w ∈D} sind homöomorph bezüglich der natürlichen Topologie von
D bzw. der natürlichen (starken) Topologie von H. Da das Dichte-Verhalten
einer Folge rein topologischer Natur ist, ist das Beispiel von der verwendeten
Metrik unabhängig.
n =< f(z),φn(z) > ist. Sei f(z) ∈ H
und (zn)n eine beliebige Folge aus D, und sei f(zn) = 0,n = 1, 2,...
Da (zn)n in D einen Häufungspunkt hat, gilt nach dem Identitätssatz für
analytische Funktionen f(z) ≡ 0 im Analytizitätsbereich B ⊃ D. Also
ist jede unendliche Menge {zn}n ⊆ D in H total, TN → 0. Falls also
z.B. (zn)n in D konvergiert, ist (zn)n in D nirgends dicht. So kann die
Dispersion δN der Folge z1,...,zN beliebig schlecht gemacht werden. D und
{K(z,w),w ∈D} sind homöomorph bezüglich der natürlichen Topologie von
D bzw. der natürlichen (starken) Topologie von H. Da das Dichte-Verhalten
einer Folge rein topologischer Natur ist, ist das Beispiel von der verwendeten
Metrik unabhängig.
Beispiel 2. Sei E = ℕ = {1, 2,...,n,...} diskret topologisiert. Sei
E∞ = E ∪{x0},x∞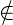 E, nach Alexandrow kompaktifiziert. Sei (an)n,an ∈
ℂ, lim n→∞an = 0,an≠0 für n = 1, 2,...,a∞ = ax∞ := 0. Sei K(x,y) = 0 für
x≠y, K(y,y) = |ay|2,x,y ∈ E
∞.
E, nach Alexandrow kompaktifiziert. Sei (an)n,an ∈
ℂ, lim n→∞an = 0,an≠0 für n = 1, 2,...,a∞ = ax∞ := 0. Sei K(x,y) = 0 für
x≠y, K(y,y) = |ay|2,x,y ∈ E
∞.
Dann ist dK(x,y) = ||K(t,x) - K(t,y)|| = (K(x,x) + K(y,y))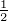 = (|ax|2 +
|ay|2)
= (|ax|2 +
|ay|2)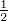 für x≠y; dK(x,x) = 0. Die Metrik dK(⋅,⋅) metrisiert die Topologie von
E∞ : Gilt lim m→∞xm = x0≠x∞, so folgt dK(xm,x0) < ϵ für m > N(ϵ), also
|axm|2 + |a
x0|2 < ϵ2 für m > N(ϵ), was d
K2(x
m,x0) = 0 für m > N(|ax0|)
nach sich zieht. Ist jedoch lim m→∞ = x0 = x∞, so bedeutet das, dass für
m > N(ϵ) dK(xm,x∞) = (|axm|2 + 02)
für x≠y; dK(x,x) = 0. Die Metrik dK(⋅,⋅) metrisiert die Topologie von
E∞ : Gilt lim m→∞xm = x0≠x∞, so folgt dK(xm,x0) < ϵ für m > N(ϵ), also
|axm|2 + |a
x0|2 < ϵ2 für m > N(ϵ), was d
K2(x
m,x0) = 0 für m > N(|ax0|)
nach sich zieht. Ist jedoch lim m→∞ = x0 = x∞, so bedeutet das, dass für
m > N(ϵ) dK(xm,x∞) = (|axm|2 + 02)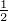 < ϵ, also lim m→∞xm = x∞, also
xm →∞ im gewöhnlichen Sinn ist.
< ϵ, also lim m→∞xm = x∞, also
xm →∞ im gewöhnlichen Sinn ist.
Der vom Kern K(x,y) über E∞ errichtete Hilbertraum H besitzt die
Orthonormalbasis φn(x),n = 1, 2,…, mit φn(n) = an, φn(m) = 0 mit
m≠n. Demgemäß gilt K(x,y) = ∑
n=1∞φ
n(x)φn(y) und H =  f(x) =
∑
n=1∞
f(x) =
∑
n=1∞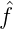 nφn(x), (
nφn(x), (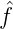 n)n ∈ l2
n)n ∈ l2 , wobei
, wobei 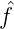 n =< f,φn > und f(m) = f(xm) ≡
n =< f,φn > und f(m) = f(xm) ≡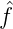 mam,f(x∞) = 0
ist. Daraus folgt sofort der Satz: Die Folge (xm)m in E∞ ist genau dann total
in H, wenn sie in (E∞,dK(⋅,⋅)) dicht ist. Dies ist genau dann der Fall, wenn
{xm,m ∈ N} = E oder = E∞ ist. Die Totalität TN und die Dispersion δN
einer Folge y1,…yN lässt sich wie folgt explizit angeben:
mam,f(x∞) = 0
ist. Daraus folgt sofort der Satz: Die Folge (xm)m in E∞ ist genau dann total
in H, wenn sie in (E∞,dK(⋅,⋅)) dicht ist. Dies ist genau dann der Fall, wenn
{xm,m ∈ N} = E oder = E∞ ist. Die Totalität TN und die Dispersion δN
einer Folge y1,…yN lässt sich wie folgt explizit angeben:
Beweis. HN = span{K(x,y1),…,K(x,yN)},
HN⊥ = span{K(x,y),y ∈ E ∞, y≠y1,…,yN}
Also ist
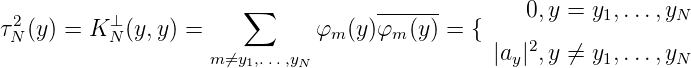
Daraus folgt TN2 = max yTN2(y) = max y≠y1,…,yN|ay|2.
Betreffend die Dispersion von y1,…,yN gilt:
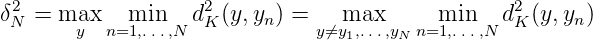
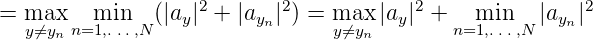
__
Bemerkung 2. Aus dem Satz folgt unmittelbar: Wenn man die Folge (yn)n aus E∞ so wählt, dass |ayn| monoton fällt, ist (yn)n bezüglich TN und δN optimal.
Es ist eine Grundaufgabe der numerischen Mathematik, das Integral einer Funktion f(x) über einen Bereich B durch ein Mittel der Funktionswerte f(xn) aus Stellen x,…,xN ∈ B näherungsweise zu berechnen:
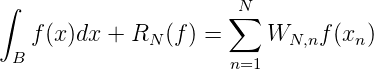
In (E,K,H) lautet eine analoge Aufgabe
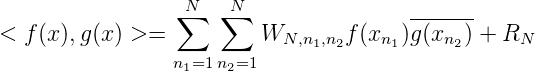
für f(x),g(x) ∈ H.
Sei x1,…,xN bzw. (xn)n eine Folge in E. Dann ist gN(t) =< g(t),KN(t,x) > KN⊥(t,x) = K(t,y)-K N(t,x),gN⊥(x) = g(x)-g N(x) =< g(t),KN⊥(t,x) > .
Definition. Die Folge (xn)n heißt g-total, wenn gN(x) schwach gegen g(x) konvergiert, gN(x) ⇁ g(x); wenn also für alle f(x) ∈ H gilt
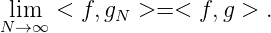
Es gilt der einfache Satz:
Beweis. Sei (xn)n g-total. Dann gilt für f(x) = g(x) :
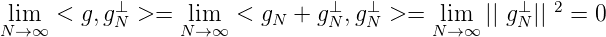
Sei umgekehrt lim N→∞||gN⊥|| = 0. Dann ist für f ∈ H
| < f,gN⊥ > |≤||f|||| g N⊥||→ 0 für N →∞.
Also gilt gN⊥ ⇁ 0. __
Beweis. Da (xn)n laut
Voraussetzung total ist, gilt g(x) = ∑
n=1∞ (n)τ
n(x) = gN(x) + gN⊥(x).
also ist lim N→∞|| gN⊥|| 2 = ∑
n>N|
(n)τ
n(x) = gN(x) + gN⊥(x).
also ist lim N→∞|| gN⊥|| 2 = ∑
n>N| (n)|2 = 0, also (x
n)n g-total. __
(n)|2 = 0, also (x
n)n g-total. __
Eine quantitaitve Relation zwischen || gN⊥|| =: T N(g) und TN = TN(K(⋅,⋅)) = max y||KN⊥(t,y)|| herzustellen ist nur mit speziellen Voraussetzungen über g(x) möglich. Es gilt jedoch der einfache Satz:
Beweis. gN⊥(x) =< g N⊥(t),K(t,x) >=< g N⊥(t),K N⊥(t,x) >, also ||gN⊥(x)|| ∞ ≤ ||gN⊥(x)|| max x||KN⊥(t,x)|| = ||g N⊥(t)||T N ≤ ||gN⊥(x)|| max x||K(t,x)|| _
Wir betrachten nun die Grundaufgabe
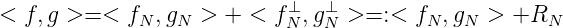
Dann ist
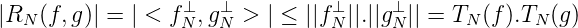
Wir stellen nun < fN(x),gN(x) > mit Hilfe des Knoten x1,…,xN dar:
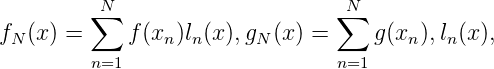
also
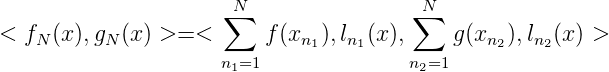
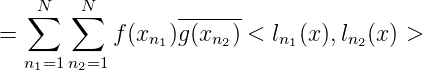
Wegen (ln1(x),ln2(x) >)n1,n2=1N = G N-1 gilt in Matrixdarstellung:
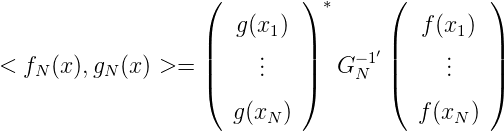
Wir hatten GN = UNDN2U N*,U NUN* = I N,DN2 = diag(λ 12,…,λ N2).
Definition. Wir nennen UN,DN das K-Eigensystem der Punkte x1,…,xN ∈ E.
Das K-Eigensystem beschreibt wesentliche Merkmale der Punkte x1,…,xN hinsichtlich der Approximation von Funktionen und Funktionalen aus (E,K,H) durch finite Ausdrücke. Jedenfalls erhalten wir
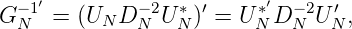
wobei UN′⋅ UN*′ = I N ist. Also ist
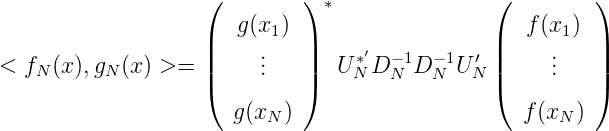
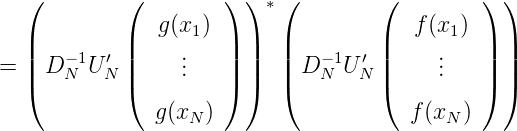
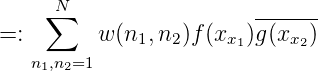
Die Komplexität der Berechnung von < fN,gN > ist O(N2), analog zur DFT.
Wir setzen mit der unitären Matrix UN′
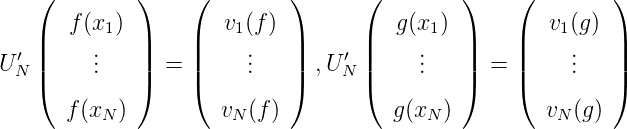
und erhalten
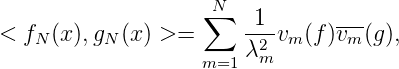
was die Rolle des Eigenwert von x1,…,xn sichtbarer macht.
Wir erhalten also
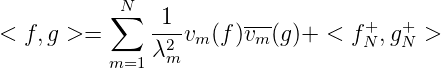
Wir merken an: RN(f,g) → 0 für N →∞, wenn gN⊥ ⇁ 0 oder f N+ ⇁ 0. Wenn gN⊥ ⇁ 0, gilt || g N⊥|| ⇁ 0 und || g N⊥|| ∞ → 0. Falls ||gN⊥|| ∞ → 0 bekannt ist, gilt gN⊥(x) → 0 für jedes x ∈ E. Das bedeutet aber g N⊥ ⇁ 0, also sind diese drei Eigenschaften äquivalent.
Man kann Ig(f) =< f,g > bei festem g ∈ H und f ∈ H als g-Integral von f ∈ H betrachten. Dann ist die Abschätzung
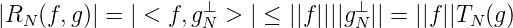
oft praktischer.
Wir konkretisieren diese Abschätzungen am Beispiel einer beliebigen kompakten Abelschen
Gruppe G mit reproduzierenden Kern vom Faltungstyp: Sei h(x) ∈ l2(G),ĥ(γ)≠0
für γ ∈Ĝ,ĥ(γ) = 1 für den trivialen Charakter γ0. Sei k(x) = h(x) *h(-x).
Darum ist k(x) = ∑
γĥ(γ)ĥ(γ)γ(x),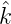 (γ) = ĥ(γ)h(γ) > 0,
(γ) = ĥ(γ)h(γ) > 0,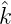 (γ0) = 1. Der Kern
K(x,y) = k(x-y) = ∑
γ
(γ0) = 1. Der Kern
K(x,y) = k(x-y) = ∑
γ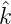 (γ)γ(x) ist positiv definit und erzeugt den Hilbertraum H
mit der ONB φγ(x) = ĥ(γ)
(γ)γ(x) ist positiv definit und erzeugt den Hilbertraum H
mit der ONB φγ(x) = ĥ(γ)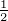 γ(x),γ ∈Ĝ.H = {f(x) = ∑
γ
γ(x),γ ∈Ĝ.H = {f(x) = ∑
γ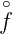 (γ)φ(x),∑
γ|
(γ)φ(x),∑
γ|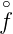 (γ)|2 < ∞}.
Es ist
(γ)|2 < ∞}.
Es ist 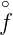 (γ)
(γ)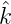 (γ)
(γ)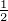 =
= 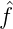 (γ). Wegen
(γ). Wegen 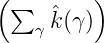 ≤
≤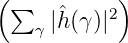 ist K(x,y) = k(x-y)
stetig. Weiters gilt ||K(x,y)|| = K(y,y)
ist K(x,y) = k(x-y)
stetig. Weiters gilt ||K(x,y)|| = K(y,y)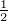 = k(y - y)
= k(y - y)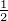 = k(0)
= k(0)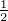 = (∑
γ
= (∑
γ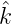 (γ))
(γ))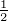 .
Die Funktionen gy(x) = K(x,y) liegen also alle auf der Kugel in H mit
dem Radius k(0)
.
Die Funktionen gy(x) = K(x,y) liegen also alle auf der Kugel in H mit
dem Radius k(0)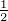 . Da die Charaktere γ ∈Ĝ die Punkte trennen, ist
dK(x,y) = || K(t,x) - K(t,y)|| eine Metrik auf G. Sei g(x) = 1 für x ∈ G, dann
ist g(x) ∈ H und für f ∈ H ist
. Da die Charaktere γ ∈Ĝ die Punkte trennen, ist
dK(x,y) = || K(t,x) - K(t,y)|| eine Metrik auf G. Sei g(x) = 1 für x ∈ G, dann
ist g(x) ∈ H und für f ∈ H ist
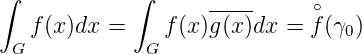
ein stetiges lineares Funktional auf H. Als Stützstellen für die Approximation des
Haarintegrals von f(x) wählen wir die Elemente einer zyklischen Untergruppe
GGN = {kx1,k = 0,…,N},HN = span{K(x,xk),k = 0,…,N - 1,xk = kx1},HN⊥
der Orthogonalraum von HN ⊆ H. KN(x,y) reproduziert HN,KN⊥(x,y)
reproduziert HN⊥,K(x,y) = K
N(x,y) + KN⊥(x,y).GN = (k((n - m)x1))m,n=0N-1 ist zirkulant und nicht singulär. Die Spalten der
Fouriermatrix FN = (wmn)
m,n=0N-1 sind die Eigenvektoren von G
N. Die
Eigenwerte von GN sind die DFT der ersten Spalten von GH. Es gilt mit
w = e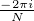 :
:
λk2 = ∑
j=0N-1k(x
1(N - j))wjk für k = 0,…,N - 1.
Sei FN = (wmn)
m,n=0N-1 und U
N = 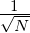 FN,UNUN* = I
N.
FN,UNUN* = I
N.
Da GN und GN-1 zirkulant sind, gilt
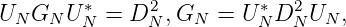
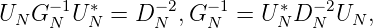
mit DN2 = diag(λ 02,…,λ N-12). Es gilt K(x,x k) = k(x - xn),k = 0,…,N - 1, und somit für die Interpolationsfunktionen, lk(x), als duale Basis von HN,lk(x) = l0(x - xk),lk(x)⊥k(x - xk), wobei
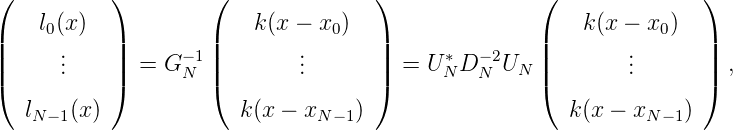
wobei es genügt, l0(x) mittels DFT zu bestimmen.
Allgemein gilt also für < fN(x),gN(x) >,f,g ∈ H, kontragradient
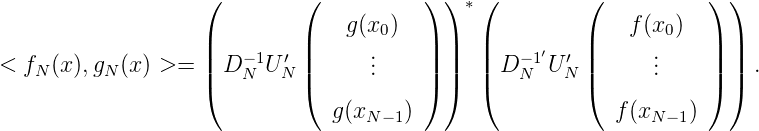
< fN(x),gN(x) > wird also durch DFT erhalten.
Im Fall des Haar-Integrals, da g(x) = 1 für x ∈ G ist ersichtlich:
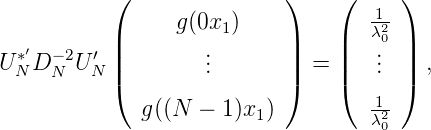
da g(xk) = 1 für k = 0,…,N - 1.
Also ist
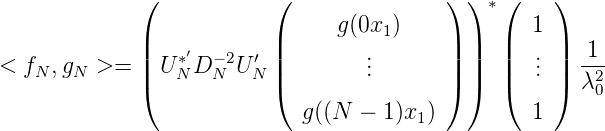
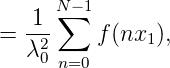
mit λ02 = ∑
n=0N-1k(nx
1). Für f(x) = g(x) = 1 ergibt sich unmittelbar
< gN,gN >= ||gN||2 = 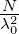 , also ||gN⊥||2 = 1 -||g
N||2 = 1 -
, also ||gN⊥||2 = 1 -||g
N||2 = 1 -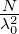 . Wir stellen
nun die λ02 unter Verwendung der Reihe k(x) = ∑
γ
. Wir stellen
nun die λ02 unter Verwendung der Reihe k(x) = ∑
γ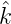 (γ)γ(x) dar: Sei
Kk = {γ ∈Ĝ : γ(x1) = e2πik∕N},k = 0,…,N - 1. Dann ist
(γ)γ(x) dar: Sei
Kk = {γ ∈Ĝ : γ(x1) = e2πik∕N},k = 0,…,N - 1. Dann ist
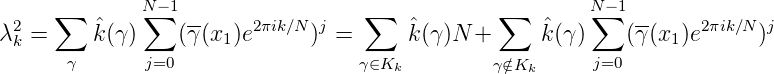
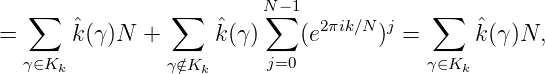
da die Charaktersummen über γ ∈ Kk bzw γ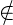 Kk den Wert N bzw 0 haben. Man
erhält übrigens auf analoge Weise
Kk den Wert N bzw 0 haben. Man
erhält übrigens auf analoge Weise
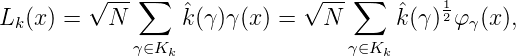
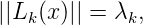
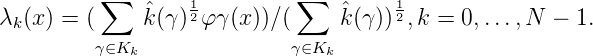
Diese Darstellung der λ0(x),…,λN-1(x) zeigt direkt die Orthonormalität dieser Basis von HN.
Wir kehren zurück zu < fN,gN >:
Wir definieren in naheliegender Weise die K-Diaphonie einer Folge
x0,…,xN-1 ∈ G:
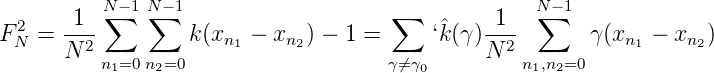
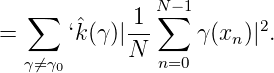
Da für xk = kx1,k = 0,…,N - 1, die Charaktersummen den Wert 0 oder N
annehmen gilt hier wegen 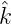 (γ0) = 1
(γ0) = 1
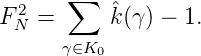
Also haben wir
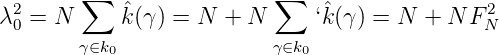
Daraus folgt
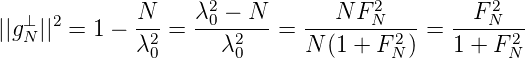
Für gut gleichverteilte xa = kx1,k = 0,…,N - 1,xa ∈ GGN, ist λ02 ~ N,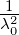 ~
~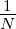 und ||g⊥||2 < F
N2. Wir erhalten also den Satz
und ||g⊥||2 < F
N2. Wir erhalten also den Satz
Satz 10. Ist f(x) ∈ H,g(x) = 1, dann ist < f,g >= ∫
af(x)dx. Ist GN
eine zyklische Gruppe GN = {kx1,k = 0,…,N - 1}, dann ist | < f,g > - <
fN,gN > | = |∫
Gfdx -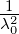 ∑
n=0N-1f(nx
1)|≤||f||||gN⊥|| = ||f||
∑
n=0N-1f(nx
1)|≤||f||||gN⊥|| = ||f||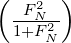
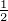 ,
wobei λ02 = N + NF
N2 = ∑
n=0N-1k(nx
1) ist.
,
wobei λ02 = N + NF
N2 = ∑
n=0N-1k(nx
1) ist.
Das Gewicht λ02 lässt sich also leicht berechnen.
Wenn man weiter spezialisiert und G = [0, 1)s mit
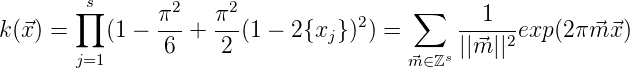
betrachtet, wobei ||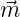 || := ∏
j=0s max(1,|m
j|) ist, erhält man diese K-Diaphonie
in Gestalt der klassichen Diaphonie
|| := ∏
j=0s max(1,|m
j|) ist, erhält man diese K-Diaphonie
in Gestalt der klassichen Diaphonie
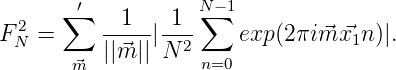
Wählt man für GN = {k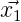 ,k = 0,…,N} beispielsweise ’gute Gitterpunkte’ bzw
’optimale Koeffizienten’ im Sinne von Hlawka und Korobow, so ergibt sich
bekanntlich
,k = 0,…,N} beispielsweise ’gute Gitterpunkte’ bzw
’optimale Koeffizienten’ im Sinne von Hlawka und Korobow, so ergibt sich
bekanntlich
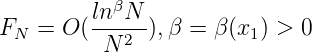
Die hier vorgestellte Methode ist nicht auf E = [0, 1)s beschränkt, sondern
ermöglicht auch, neben dem ∫
afdx auch allgemeinere Funktionale
< f,g >= ∫
fdg(x) zu betrachten und beleuchtet auch die Rolle der Eigenwerte
λ0,…,λn-1 einer Folge von Punkten xh,h = 1,…,N.
[1] Aronszajn, N.: Theorie of reproducing kernels. Trans. Hm. Math. Soc. 68, 1950.
[2] Meschkowski, H.: Hilberträume mit Kernfunktion. Grundlehren, Band 113, Springer 1962.
[3] Niederreiter, H., Kuipers, L.: Uniform Distribution of Sequences Wiley 1974.
[4] M. Drmota, R.F. Tichy: Sequences, Discrepancies and Applikations. Lecture Notes in Mathematics 1651, Springer 1997
[5] Korobow, N.M.: Zahlentheoretische Methoden in der Numerischen Mathematik. Fismatgis 1962, Russisch.