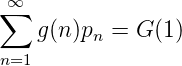
Keywords: Uniform distribution of sequences, Discrepancy, Koksma’s theorem, Helly’s theorem, Gauge Integral, Banach space valued sequences, continued fractions, Minkowski’s question mark funktion ?(x).
Zusammenfassung: Konvergente Folgen komplexer Zahlen werden als stetige Funktionen betrachtet, sodaß die Gleichverteilung von Folgen aus ℕ bezüglich eines Borelschen Wahrscheinlichkeismaßes auf ℕ betrachtet werden kann. Solche stetige Funktionen lassen sich als Eichmaßintegrale bezüglich der betrachteten Wahrscheinlichkeitsmaße darstellen. In weiterer Folge wird die Totalvariation von Funktionen erklärt und es wird der passende Diskrepanzbegriff für Folgen natürlicher Zahlen verwendet, um einen Satz von Koksma-Typ zu beweisen. Der Banachraum der Funktionen von beschränkter Variation und der Dualraum werden beschrieben und es wird ein Helly’scher Auswahlsatz bewiesen. Schließlich werden die Resultate in gewissem Ausmaß für Banachraumwertige Funktionen formuliert und es wird der Dualraum dieses Banachraumes bestimmt. Die zu erwartende und naheliegende Erklärung von Lp- Diskrepanzen für Folgen natürlicher Zahlen führt zwangslos zu einem Begriff der Variation q-ter Ordnung für Funktionen auf ℕ und eine Abschätzung DM(p)V (R)(G) ≥|R M(G)|. Dieser Variationsbegriff ist analog zu einem Resultat über absolut stetige Funktionen von F. Riez.
Sei ℕ diskret topologisiert und ℕ∞ die Alexandrow-Kompaktifizierung. Die Menge C(ℕ∞) besteht als Menge der auf ℕ∞ stetigen Funktionen aus den konvergenten komplexwertigen Folgen, C0(ℕ∞) entsprechend die Menge der Nullfolgen. C(ℕ∞) und C0(ℕ∞) sind ausgestattet mit der uniformen Norm ||G||u = sup{|G(n)|,n ∈ ℕ}, Banachräume. Wir benöigen einen weiteren Typ von Banachraum:
Seien für ⋃ Ik = ℕ,k = 1, 2,..., Ik = [ak,bk] = {n : ak ≤ k ≤ bk},a1 = 1,ak+1 = bk+1,bIk = ℕ. Falls es nur endlich viele Ik gibt, ist sinngemäß das letzte bn gleich dem unendlich fernen Punkt. Sei B die Familie der Menge Ik,k = 1, 2,...,B = {Ik,k = 1, 2,...} und C(B) die Menge der konvergenten Folgen G(n) mit G(n) =const. auf jeweils Ik,k = 1, 2,..., sowie C0(B) die Menge der Nullfolgen in C(B), welche Banachsche Teilräume von C(ℕ∞) bzw. . C0(ℕ∞) sind.
Sei nun P eine Wahrscheinlichkeitsverteilung auf ℕ∞, ∑ n=1∞p n = 1,p∞ = 0. Sei g = (g(n))n eine Folge komplexer Zahlen, sodaß die Reihe
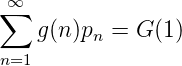
konvergiert. Also sind die Reihen
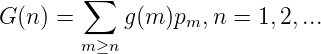
konvergent und es gilt lim n->∞G(n) = 0. Somit ist G = (G(n))n ∈ C0(ℕ∞) Die Folge B(P) = (Ik(P))n der Intervalle, wo G konstant ist, ergibt sich wie folgt:
Sei a1 = 1 und b1 gleich der kleinsten natürlichen Zahl n mit pn > 0. Damit ist I1 = I1(P) = [a1,b1] definiert. Angenommen, die Intervalle I1,...,Ik = [ak,bk] sind bereits definiert, dann sei ak+1 = bk+1 und bk + 1 gleich der kleinsten natürlichen Zahl n ≥ ak+1 mit pn > 0. Wenn es keine solche Zahl n gibt, sei bk+1 = ∞. Damit ist das Intervallsystem B(P) = (Ik(P))k erklärt. Offensichtlich ist (G(n))n = G genau auf den Intervallen Ik = Ik(P) konstant.
Wegen G(n) = g(n)pn + ∑ m≥n+1g(m)pm = g(n)pn + G(n + 1) gilt g(n) = (G(n) - G(n + 1))∕pn falls pn > 0. Falls pn = 0, ist g(n) unbestimmt. Das P-Maß der Menge der natürlichen Zahlen n mit pn = 0 ist offensichtlich Null. Also ist g(n) = (G(n),...,G(n + 1))∕pn. P - fast überall definiert. P ist ein Borelsches normiertes Maß auf ℕ bzw ℕ∞ und führt zu dem Integral ∫ ℕ∞f(n)dP(n) = ∫ ℕf(n)dP(n). f = (f(n))n ist genau dann integrierbar, wenn |f| integrierbar ist. Es gilt offensichtlich im Falle der Integrierbarkeit
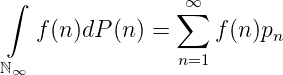
Definition. G′(n) := (G(n) -G(n + 1))∕pn für pn > 0. Für pn = 0 ist G′(n) nicht definiert.
Also ist G′(n) für P- fast alle n ∈ ℕ definiert und es gibt G(n) = ∑ m≥nG′(m)pm, wobei i.A. G′ nicht integrierbar ist, also die Reiche nicht absolut konvergiert ist.
Üblicherweise bezeichnet man die Totalvariation einer Folge f = (f(n))n mit ∑ n=1∞|f(n + 1) - f(n)|. Falls V (f) = ∑ n=1∞|f(n + 1) - f(n)| < ∞, so ist wegen
|f(n+p)-f(n)| = |f(n+1)-f(n)+...+f(n+p)-f(n+p-1)|≤∑ n=1∞|f(n+p)-f(n+p-1)|→ 0 für n →∞, die Folge also konvergent. Sei nun G ∈ V ar(N) := {F : ∑ n=1∞|F(n)-F(n+1)| < ∞}
Sei weiters P ein strikt positives Maß, also pn > 0 für n = 1, 2,.. . Dann ist G′(n) = (G(n) -G(n + 1))∕pn überall definiert und P- integrierbar und es gilt mit G′(n) = dG(n)|dP
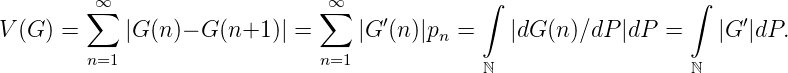
Speziell gilt, dass die Reihe
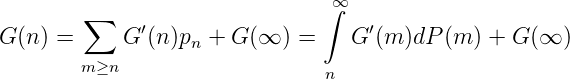
absolut konvergiert, sodaß sich das Analogon zum Hauptsatz der Differential und Integralrechnung ergibt:
Satz 1. Falls P strikt positiv ist, ist G(n) = ∫ n∞G′(m)dP(m)+G(∞) genau dann, wenn G von beschränkter Variation ist. Dann ist V (G) = ∫ n∞|G′|dP.
Wir werden von der Voraussetzung pn > 0 für n = 1, 2,... absehen können.
Beweis. Das Integral
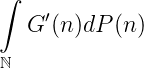
existiert genau dann, wenn ∑ n=1∞|G′(n)|p n < ∞. Genau dann ist G(n) = ∑ m≥nG′(n)pn + G(∞) = ∫ n∞G′(m)dP(m) __
Zur Definition von Eichmaß-Integralen betrachten wir eine dissunkte Zerlegung von ℕ durch B = {Ik,k = 1, 2,..},Ik = [ak,bk],∪kIk = ℕ
Definition. Das Maß P = (pn)n heißt verträglich mit B, wenn pbk > 0 und pn = 0 für ak ≤ n < bk. Für ak = bk ist also pak = pbk > 0.
Sei nun G ∈ C(B), also aus dem Banachraum der auf den Intervallen Ik konstanten Folgen, und sei P ein mit der Zerlegung B kompatibles Wahrscheinlichkeitsmaß auf ℕ. Dann ist
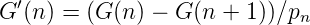
genau an den Stellen bk,k = 1, 2,.., definiert, also P-fast überall erklärt. Es gilt also
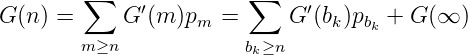
Da die Reihe i. A. nicht absolut konvergiert, ist i. A. G(n) nicht durch ein P- Integral darstellbar.
Dies gibt Anlass, das Eichmaß-Integral von G′ bezüglich P zu definieren:
Definition. Für G ∈ C(B) ist
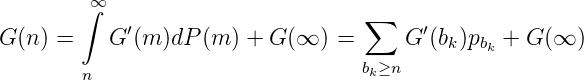
das Eichmaßintegral von G’ bezüglich P.
Bemerkung: ∮ soll an das Gauge-Integral erinnern.
Es gilt also der
Der Hauptsatz der Differential- und Integralrechnung mittels Eichmaßintegral gilt auf C(B) genau für die zu B kompatiblen Maße P.
Folgerung: Eine beliebige stetige Funktion G ∈ C(ℕ∞) ist beüglich P genau dann als Eichmaßintegral, bezeichnet durch ∮
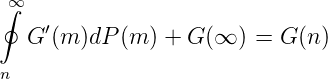
darstellbar, wenn die einzige P-Nullmenge die leere Menge ist. Dies ist genau dann der Fall, wenn pn > 0 für n = 1, 2,...
Wir beweisen nun einen Helly’schen Auswahlsatz für die Funktionen mit beschränkter Totalvariation.
Es gilt zunächst der
Satz 3. Ist G ∈ C(ℕ∞) eine reelle Funktion von beschränkter Variation, so ist G die Differenz zweier monoton fallender Funktionen und umgekehrt.
Beweis. Da G von beschränkter Variation ist, gilt für ein strikt positives Maß
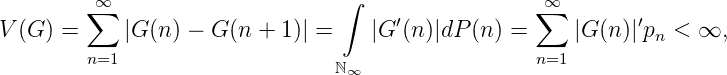
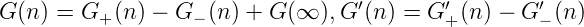
Folglich ist G+(n) = ∫ m≥nG′+(n)dP(n) und G-(n) = ∫ m≥nG′-(n)dP(n) monoton fallend, wobei ohne Beschränkung der Allgemeinheit C(∞) = 0 ist.
Ist umgekehrt G(n) = G1(n) - G2(n) für n = 1, 2,.., G1,G2 ∈ C(ℕ∞), und ist G1,G2 monoton fallend, so ist
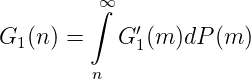
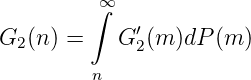
mit G1′,G2′≥ 0 und V (G) = V (G1) + V (G2) < ∞ _
Wir geben einen zweiten Beweis für diesen Satz, der nicht auf strikt positive Maße P zurück greift:
Beweis.
Sei V ab(G) = ∑ n=xδ|G(n) - G(n + 1)| und V (G) = V 1∞(G) = ∑ n=1∞|G(n) - G(n + 1)|. Sei π(x) = V x∞(G) = ∑ n=x∞|G(n) - G(n + 1)|, dann ist π(x) monton fallend gegen Null. Sei v(x) = π(x)-G(x). Wir zeigen, dass v(x) ebenfalls monoton gegen Null geht: Sei 1 ≤ x < y < ∞,x,y ∈ ℕ. Dann gilt:
![y∑-1
v(y)- v(x) = π(y)- π(x)- [G(x )- G (y)] = - [ |G (n)- G (n+1 )|]- [G (x)- G (y )]
n=x](4.4.21-Skript-214x.png)
Nun ist
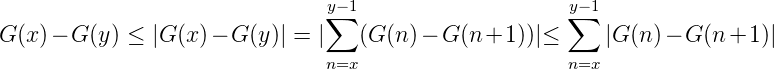
sodass gilt
![v(y) - v(x) = π(y) - π(x) - [G(x ) - G (y)] ≤ 0.](4.4.21-Skript-216x.png)
__
Also ist G(x) = π(x) - v(x) als Differenz der monoton gegen Null fallenden Funktionen π(x) und v(x) dargestellt, sofern V (G) < ∞ und lim x→∞G(x) = 0. Falls lim x→∞ = G(∞) ∈ ℝ, ist statt G(x) die Funktion G(x) - G(∞) zu betrachten.
Bemerkung: Der Satz gilt sinngemäß für die Räume C(B) und C0(B) ebenso.
Für den Beweis eines Helly’schen Auswahlsatzes benötigen wir zwei einfache Hilfssätze.
Hilfssatz 1: Sei eine unendliche Familie von Funktionen G(x) und ℕ∞ gegeben, die gleichmäßig beschränkt ist, ||G(x)||u ≤ K, so kann man eine punktweise konvergente Folge Gm(x) auswählen, deren Limes ebenfalls durch K beschränkt ist.
Beweis. Anwendung des Kompaktheitstheorems von Tichonow. __
Hilfssatz 2: Ist (Gm(x))m eine Folge fallender Funktionen, die punktweise konvergiert und gleichmäßig beschränkt ist, |Gm(x)|≤ k, für m = 1, 2,...,x ∈ ℕ, dann ist G(x) = lim m→∞Gm(x) ebenfalls monoton fallend. Der Sachverhalt ist offensichtlich.
Die Totalvariation V (G) ist eine Halbnorm auf C(ℕ∞) bzw. C(ℕ). Auf C0(ℕ∞) bzw. C0(ℕ) ist
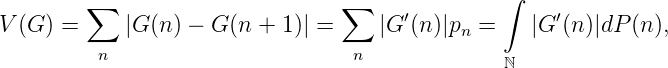
also ist V (G) die L1(ℕ∞,P)- Norm von G′:
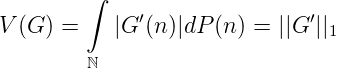
Setzen wir V ar0(ℕ∞) := {G ∈ C0(ℕ) : V (G) < ∞}, so ist der Dualraum
V ar0(ℕ0)′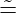 L∞(ℕ,P). Ist weiters V ar(ℕ∞) = {G ∈ C(ℕ∞) : V (G) < ∞}, so ist
||G||v := V (G) + |G(∞)| eine Norm und die angesprochenen Räume sind
Banachräume.
L∞(ℕ,P). Ist weiters V ar(ℕ∞) = {G ∈ C(ℕ∞) : V (G) < ∞}, so ist
||G||v := V (G) + |G(∞)| eine Norm und die angesprochenen Räume sind
Banachräume.
Wir beweisen nun den folgenden Satz als diskrete Variante des Auswahlsatzes von Helly:
sede in den beiden (Halb-) Normen ||⋅||n und ||⋅||v beschränkte Menge M von Funktionen besitzt eine Teilfolge die vage gegen eine Funktion von beschränkter Totalvariation konvergiert.
Beweis. Da die Menge von Funktionen gleichmäßig etwa durch K > 0 beschränkt ist, gibt es zur Folge Gm in M, eine punktweise konvergente Teilfolge, die wir der Einfachheit halber auch mit Gm bezeichnen. Sei Gm(n) = Am(n) + iBm(n),n = 1, 2,... in Realteil und Imaginärteil zerlegt. Die Normen ||Am||u,||Am||v,||Bm||u,||Bm||v sind ebenfalls durch K beschränkt. Wir zerlegen nun die Am und Bm in Differenzen zweier fallender Folgen:
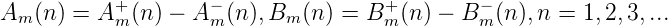
Die Funktionenfolge Am+ hat nach dem Satz von Tichonow eine vage konvergente Teilfolge Ami+. Deser punktweise Limes sei A ∞+ bezeichnet. Wir werden uns diese Vorgangsweise sukzessive ohne Änderung der Indizierung durch ms,s = 1, 2,..., auf Am-,B m+ und B m- an und erhalten so die vagen Limiten A∞-,B ∞+,B ∞-, wobei die Folgen nach dem Hilfssatz 2 alle monoton fallend sind. Folglich sind A∞ := A∞+ - A ∞- und B ∞ := B∞+ - B ∞- und auch G ∞ := A∞ + iB∞ von endlicher Totalvariation und G∞ ist vager Limes der Teilfolge Gmi, was zu zeigen war. __
Bemerkung: Der Satz gilt in gleicher Weise für die Räume C(B) und C0(B).
Beweis. C(B) ist der Raum der auf den Intervallen B = {Ik = [ak,bk],k = 1, 2,...} konstanten konvergenten Folgen G = (G(k))k, ausgestattet mit der uniformen Norm mit der vogen Konvergenz, wobei ∪Ik = ℕ,ak+1 = bk + 1,C(B) ist entsprechend. Sei s = {sk = [k,k],k = 1, 2,..}. s ist endlich, genau wenn B endlich ist. Sei φ(G) = H, wobei H(k) = G(δk),k = 1, 2,.... Sei D(ℕ) = {H,H(k) konvergent} und D0(ℕ) der Teilraum der Nullfolgen, seweils ausgestattet mit der uniformen Norm bzw. der vagen Topologie. Die Abbildung φ ist eine Isometrie zwischen C(B) und D(s) bzw C0(B) und D0(s) und eine toplineare Isomorphie der Räume bezüglich der vagen Konvergenz.
Damit ist klar, dass der obige Auswahlsatz auch für C(B) und C0(B) gilt. __
Sei nun P ein Wahrscheinlichkeitsmaß auf ℕ bzw ℕ∞ : P = (pn)n,pn ≥ 0,∑ npn = 1,p∞ = 0 sei vorausgesetzt. Das Integral der Funktion G bezüglich des Maßes P ist dann
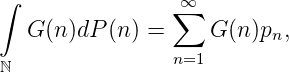
falls
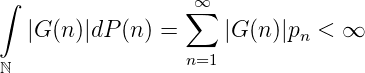
Definition. Die Folge xm,m = 1, 2,..,xm ∈ ℕ heißt P-verteilt oder gleichverteilt zum Maß P, wenn für sedes n = 1, 2,... gilt
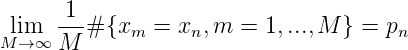
Es ergibt sich sofort der erwartete
Beweis.
Sei G(∞) = lim n→∞G(n). Da
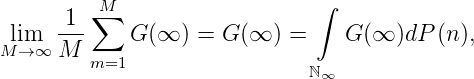
betrachten wir ohne Beschränkung der Allgemeinheit Funktionen G ∈
C0(ℕ),||G||n, also lim n→∞G(n) = 0. Falls ||G|| = 0, ist nichts zu beweisen.
Sei also ||G|| > 0. Sei N0(ϵ) so groß, dass für alle n > N0(ϵ) gilt: |G(k)| < 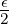 .
Sei M0 so groß, dass für alle M > M0(N0,ϵ,||G||k) gilt:
.
Sei M0 so groß, dass für alle M > M0(N0,ϵ,||G||k) gilt: 
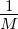 ∑
m=1M#{x
m =
pn}- pn
∑
m=1M#{x
m =
pn}- pn <
< 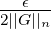 für n = 1,...,N0(ϵ).
für n = 1,...,N0(ϵ).
Dann ist für M > M0 : 
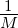 ∑
m=1MG(x
m) - ∑
n=1∞G(n)p
n
∑
m=1MG(x
m) - ∑
n=1∞G(n)p
n ≤
≤
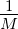 ∑
m=1MG(x
m)-∑
n=1N0(ϵ)G(n)p
n
∑
m=1MG(x
m)-∑
n=1N0(ϵ)G(n)p
n + ∑
n>N0(ϵ)|G(n)|pn ≤
+ ∑
n>N0(ϵ)|G(n)|pn ≤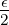
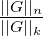 +
+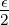 = ϵ.
= ϵ.
Also gilt lim n→∞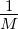 ∑
m=1MG(x
m) = ∫
ℕG(n)dP(n). Die Umkehrung folgt
sofort, wenn man Gk(n) = δkn,k = 1, 2,... betrachtet. Dann ist offensichtlich
∑
m=1MG(x
m) = ∫
ℕG(n)dP(n). Die Umkehrung folgt
sofort, wenn man Gk(n) = δkn,k = 1, 2,... betrachtet. Dann ist offensichtlich
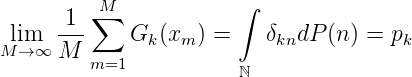
__
Wir kommen nun zu einem Diskrepanzbegriff für Folgen x1,x2,...,xm ∈ ℕ bezüglich eines Wahrscheinlichkeitsmaßes P auf ℕ: Sei wieder B = B(P) = {[ak,bk]k = 1, 2,...} sodass ak+1 = δk + 1, und pbk > 0,pn = 0 für ak ≤ k < bk. B definiert den Banachraum stetiger Funktionen G auf ℕ∞, die auf den Intervallen Ik konstant sind.
Wir betrachten für G ∈ C(B)
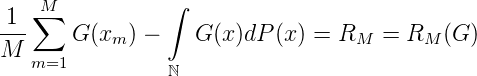
Da RM(G) = RM(G - G(∞)) gilt, betrachten wir ohne Beschränkung der Allgemeinheit Funktionen G(x) mit G(∞) = lim x→∞G(x) = 0. Wir setzen weiters voraus, dass G(x) von beschränkter Variation is. Das ist genau dann der Fall, wenn
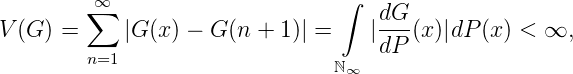
wobei dG∕dP fast überall definiert ist. Also ist die Reihe
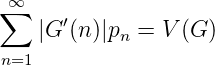
konvergent und es gilt
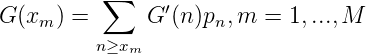
Also ist mit χ[1,k](x) als charakteristische Funktion von [1,k] ⊆ ℕ:
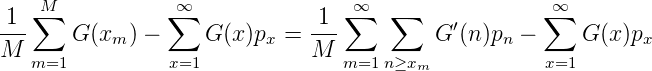
 - (p1 + ...+ pk))G (k)pk = RM
k=1 m=1](4.4.21-Skript-246x.png)
Also gilt mit der Hölderschen Ungleichung
 - (p1 + ...+ pk)| |G ′(x)|dP (x)
k M m=1 ℕ](4.4.21-Skript-247x.png)
Definition.
![∑M
sup |-1- χ (xm ) - (p1 + ...+ pk)| =: D * ,
k M m=1 [1,k] M](4.4.21-Skript-248x.png)
DM* ist als P-Diskrepanz der Folge x 1,...,xm zu bezeichnen.
Es gilt also der dem Satz von Koksma ähnliche
Wir zeigen nun den
Beweis.
1. Aus der P- Verteilung der Folge (xm)m folgt DM → ∞. Sei L > 0, wir betrachten die Zahlen l∕L ∈ [0, 1],l = 1, 2,..,L. Seien xL,l so, dass
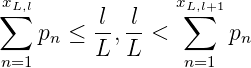
Ist x1,...,xM ∈ ℕ gegeben, so sei
 = ------------
M m=1 M](4.4.21-Skript-251x.png)
Sei ΔM = max l=1,...,L|FM(xL,l) - F(xL,l)| = ΔM,L. Es ist FM(x) - F(x) =
FM(x) - F(xL,l+1) + F(xL,l+1) - F(x),F(xL,l+1) - F(x) < 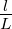
FM(x)-F(x) = (FM(x)-FM(xL,l))-(F(x)-F(xL,l))-(F(xL,l)-FM(xL,l))
Im Intervall [xL,l,xL,l+1] ist |FM(x)-F(xL,l+1)|≤ ΔM und es ist F(xL,l+1) = F(xL,l) + 1∕L. Also ist
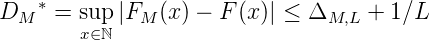
Sei L > ⌊1∕ϵ⌋ + 1, dann ist 1∕L < ϵ. Da (xn)mP-verteilt ist, gibt es ein M(ϵ,L), sodass für alle M > M(ϵ,L) gilt: für l = 1,...,L ist FM(xL,l) - F(xL,l)| < ϵ. Also ist für M > M(ϵ,L) :
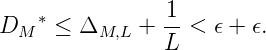
Also ist die Notwendigkeit gezeigt.
2) Dass aus DM* → 0 für M →∞ die P-Verteilung der Folge (x m)m folgt ist unmittelbar einzusehen:
Die Funktionen G ∈ C(P) bzw. G ∈ C0(P) die schließlich konstant bzw. schließlich Null werden sind einerseits von endlichen Totalvariationen V (G) = ∑ n=1N-1|G(n) - G(n + 1)| + |G(N)| < ∞, und sind andererseits uniform dicht in den Räumen. Also folgt aus DM → 0 und der Koksma-Ungleichung auch dass (xm)mP-verteilt ist. __
Bemerkung: Sei G eine stetige Funktion von ℕ∞ in den Banachraum
(R,||⋅||R). Dann ist V (G) = ∑
n=1N-1||G(n) - G(n + 1)||
R definiert. Es lassen
sich alle Ergebnisse sinngemäß beweisen, sedoch ist ein Auswahlsatz vom
Helly’schen Typ nicht sichtbar. Es gilt zum Beispiel auch hier
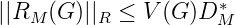
Ebenso gelten die Aussagen über Gauge-Integrale für Banachraumwertige Funktionen. Der Beweis wird später unter allgemeinen Voraussetzungen erbracht werden.
Der Vollständigkeit halber zeigen wir noch, dass fast alle Folgen P- gleichverteilt sind, wenn auch weder das Resultat noch der Beweis überraschend ist: In der Darstellung der Diskrepanz DM* der Folge x 1,...,xm,..,xM
 - (p1 + ...+ pk)|
M k M m=1](4.4.21-Skript-256x.png)
ist offenbar
 = FM (k),(p1 + ...+ pk) = F (k)
m=1](4.4.21-Skript-257x.png)
die empirische Verteilung FM(k) der x1,...,xM ∈ ℕ mit F(k) die
P-Verteilungsfunktion. Wir statten Ω = {X = (n1,n2,...,nm,...)} = ∏
m=1∞ℕ mit
dem Produktmaß P∞ = ∏
m=1∞P aus. Dann ist die m-te Komponente x
m
des zufälligen Punktes x ∈ Ω eine P-verteilte Zufallsvariable und die
x1,x2,...,xM,... sind unabhängig und identisch verteilt. Aus dem Satz von
Gliwenko (”Hauptsatz der math. Statistik”) folgt sofort: Mit Wahrscheinlichkeit 1
gilt
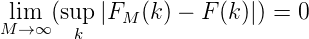
Wir wenden nun den Satz vom iterierten Logarithmus an (die Funktionen aus C(ℕ∞) an: Da G ∈ C(ℕ∞) stetig auf ℕ∞ und daher beschränkt ist, gilt D2(G) = E(|G|2) - E2(G) < ∞. Dann gilt für fast alle zufälligen Punktfolgen (xm)m und G ∈ C(ℕ∞)
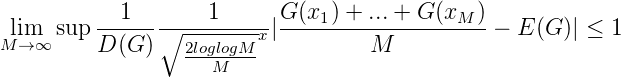
Ergänzend bestimmen wir den Dualraum des Raumes der Banachraumwertigen Funktionen C(R) mit Definitionsbereich ℕ bzw. ℕ∞. Sei also C(R) die Menge aller Folgen (G(n))n, mit Werten im Banachraum (R,||⋅||R), die im Sinne der starken Konvergenzen von R konvergent sind. Wir statten C(R) mit der uniformen Norm aus:
Definition. ||G||u = sup n∈ℕ||G(n)||R =: Nu(G) für G ∈ C(R). Damit wird C(R) zu einem Banachraum. Sei R′ der duale Raum von R als Raum aller stetigen Funktionale φ von R. Sei Φ = (φn)n eine Folge aus R′. Wir bezeichnen die Norm auf R′ mit
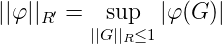
Definition. l1(R′) := {Φ = (φn)n,yn ∈ R′ : ∑
n||φn||R′ < ∞}
||Φ||1 := ∑
n||φn||R′ =: N1(Φ)
Die Beweise, dass C(R),C0(R),l1(R′) unter den angegebenen Normen Banachräume sind, sind analog zu den bekannten Beweisen für C(ℕ),C0(ℕ) und l1. Wir beweisen nun den folgenden
Beweis. Sei φn ∈ R′,n = 1, 2,.... Wegen
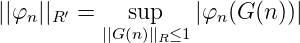
gibt es zu ϵ > 0 ein Gϵ(n) mit ||Gϵ(n)||R = 1, sodass
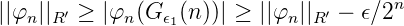
Durch Multiplikation von Gϵ(n) mit einer geeigneten Zahl |z| = 1 erreicht man ohne Bezeichnungsänderung
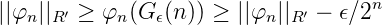
Sei nun Φ = (φn)n ∈ l1(R′), dann ist Φ stetig auf C(R):
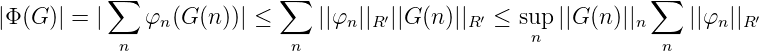
Wir führen den Beweis des Satzes in drei Schritten:
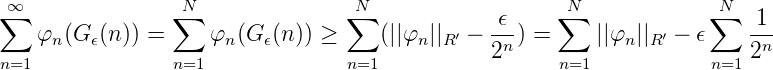
Also gilt für N →∞:
∑ n=1N||φ n||R′- ϵ ≤||Φ||D(R)′ ≤∑ n=1∞||φ n||R′ für ϵ > 0.
Also gilt: Ist Φ ∈ l1(R′), so ist ||Φ||D(R)′ = ∑ n=1N||φ n||R′ und somit ist diese Abbildung l1(R′) → D(R)′ eine Isometrie, also insektiv.
Sei nun Ψ ∈ D(R)′ beliebig und φn die Einschränkung von Ψ auf c0,n(R) := {(G(m))m : G(m) = 0 für n≠m}. Offensichtlich ist c0,n(R) ≃ R und es gilt
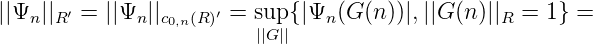
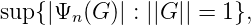
wobei Ψn(G) = Ψn(G(n)), da nun die Werte G(n) bei Ψn(G) zählen. Auf D(R) ist dann für G ∈ D(R) und Ψ ∈ D(R)′ : Ψ(G) = ∑ nΨn(G(n)), wobei die Summe endlich ist. Sei wieder Gϵ(n) ∈ R wie oben gewählt. Dann ist laut Konstruktion
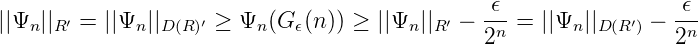
Dann ist
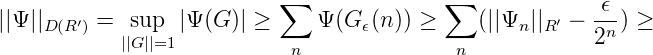
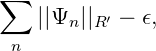
wobei die Summen seweils endlich sind. Also gilt für Gϵ = (Gϵ(1),Gϵ(2),...,Gϵ(N),...) mit N →∞ ebenfalls
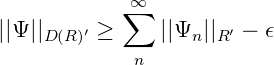
für alle ϵ > 0. Also ist ||Ψ||D(R)′ ≥ ∑ n=1∞||Ψ n||R′ und wegen ||Ψ||D(R)′ ≤ ∑ n=1∞||Ψ n||R′ folgt ||Ψ||D(R)′ = ∑ n=1∞||Ψ n||R′ und Ψ(G) = ∑ n=1∞Ψ n(G(n)) für G ∈ D(R).
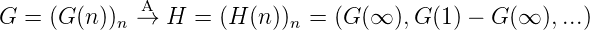
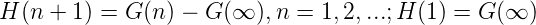
Die Umkehrabbildung A-1 ist H = (H(n))
n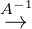 G = (G(n))n mit
G(n) = H(n + 1) + H(1) n = 1, 2,...
G = (G(n))n mit
G(n) = H(n + 1) + H(1) n = 1, 2,...
Die Abbildung A ist ein toplinearer Isomorphismus C(R) → C0(R). Die duale Abbildung zu A ist A′ : C0(R)′→ C(R)′ : Sei Φ ∈ C0(R)′, dann Φ(AG) = (A′Φ)(G) mit Φ = (φn)n ∈ l1(R′). A′ ist ebenfalls toplinear und A′Φ ∈ C(R)′. G(∞) = lim n→∞G(n). Dann ist mit Φ = (φn)n
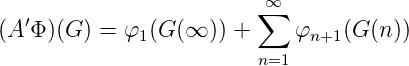
die Reihendarstellung des Funktionals, wobei ∑ n||φn||R′ < ∞.
Wir zeigen nun, dass A′ eine Isometrie ist: C0(R)′≃ C(R)′ :
Einerseits gilt
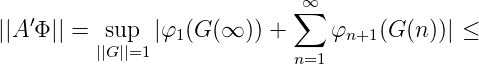
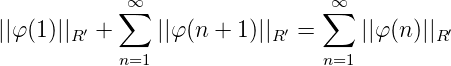
Sei wieder Gϵ(n) so gewählt, dass für n = 1, 2,... und n = ∞
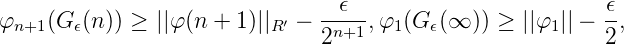
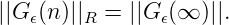
Dann ist
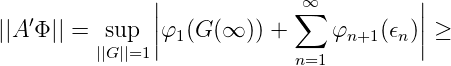
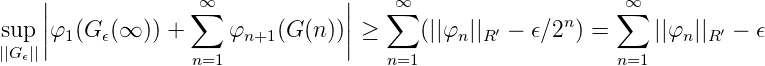
Also gilt für alle ϵ > 0:
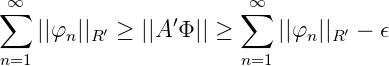
Es gilt also ∑ n=1∞||φ n||R′ = ||A′Φ||, was die Isometrie von A′ bedeutet.
Damit ist gezeigt, dass C(R)′ ≃ C0(R)′ ≃ l1(R′) und der Satz ist bewiesen.
Bemerkung 1: Für R = ℂ ist der Satz bekannt. Der Beweis ist einfach, da ℂ reflexiv ist.
Bemerkung 2: Sei C(R,B) = C der Raum der R-wertigen konvergenten Folgen G = (G(n))n, die auf den Intervallen Ik = [ak,bk],ak+1 = bk + 1,∪kIk = ℕ,I = {Ik,k = 1, 2,...}, konstant sind, dann ist C′ = l1(B), wobei l1(B) = l1(R′,B) der Raum der R′-wertigen Folgen ist, ∑ n||φn|| < ∞, und φn = 0 für n ∈ [ak,bk - 1],k = 1, 2,.... Der Beweis wird aus Raumgründen und Analogiegründen hier nicht gegeben. Man sieht auch sofort, dass C′≃ l1(R′), falls C unendlich dimensional ist, sonst ist der Satz trivial.
Wir betrachten nun die Gleichverteilung auf ℕs: Sei der diskret topologisierte Raum ℕs durch Adsunktion von X ∞ nach Alexandrow kompaktifiziert . Sei WK = {X = (x1,...,xs) ∈ ℕs : x 1,..,xs < K} und (ℕs) ∞ := ℕs ∪{X ∞}. Dann ist für K = 1, 2,... das Mengensystem ⋃ K(X∞) = (ℕs) ∞- Wk eine Umgebungsbasis von X∞. Wir metrisieren nun (ℕs) ∞ auf einfache Weise: sei (an)n eine gegen Null fallende Folge, an > am für m > n. Dann sei für X = (x1,...,xs) und Y = (y1,...,ys) ∈ ℕs d(X,Y ) := max i=1,...,s|axi - ayi| und sei d(X,X∞) := min i=1,...,saxi.
Dann metrisiert d(⋅,⋅) den Raum (ℕs) ∞. Ist G : (ℕs) ∞ → ℂ, so ist G für alle X ∈ ℕs stetig. G ist in X ∞ genau dann stetig, wenn es zu ϵ > 0 ein M(ϵ) bzw. ein δ(ϵ) gibt, sodass für alle X = (x1,...,xs) mit max xi > M bzw min axi < δ gilt: |G(X) - G(X∞)| < ϵ.
Definition. C((ℕs) ∞),C0((ℕs) ∞) sind der Raum der stetigen Funktionen auf (ℕs) ∞ bzw. der stetigen Funktionen mit G(X∞) = 0. Es sind dies die im Sinne der Topologie von (ℕs) ∞ konvergenten (Null-) Folgen.
Wir zerlegen nun ℕs in Boxen: Sei a 1 = 1, und ak ≤ bk für k = 1, 2,...,ak+1 = bk + 1,Ik = [ak,bk],∪kIk = ℕ. Falls es nur endlich viele In gibt, ist das letzte Ik = {n ≥ k}. Sei Ik1,...,ks = Ik1 ×Ik2 ×...×Iks. Dann zerfällt ℕs in das System B der Boxen Ik1,...,ks,k1,k2,...,ks = 1, 2,....
Definition. Sei C(B) bzw. C0(B), die Menge der G ∈ C((ℕs) ∞), bzw. G ∈ C0((ℕs) ∞), die auf den Ik1,...,ks ∈ B konstant sind.
Sei nun wieder P = (pn)n eine Wahrscheinlichkeitsverteilung auf ℕ und Ps = (pn1,pn2,...,pns)n1,...,ns das Produktmaß, Ps(X∞) := 0.
Sei a1 = 1 und b1 gleich dem kleinsten n ≥ 1 mit pn≠0. Ist bereits Ik = [ak,bk] definiert, so sei ak+1 = bk+1 und bk+1 gleich dem kleinsten n ≥ bk, sodass pn > 0. Dies führt zu einem Ps-Boxensystem Bs = {Ik1,...,Iks,k1,k2,...,ks = 1, 2,...}, sodass auf Ik1,...,Iks gilt pbk 1 ⋅ pbk2 ⋅ ... ⋅ pbks ≥ 0 und pl1 ⋅ pl2 ⋅ pls = 0 für ak1 ≤ l1 < bki,i = 1,...,s.
Die unendliche Reihe ∑ x∈ℕsb(X) komplexer Zahlen ist konvergent, wenn die Folge der Partialsummen SM = ∑ max xi∈Mb(x1,x2,...,xs) für M →∞ konvergiert. Das ist genau dann der Fall, wenn mit S = lim SM die Folge
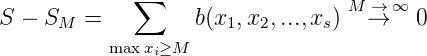
Sei X ≥ Y , wenn xi ≥ yi für i = 1,...,s.
Definition. g(X) : ℕs → ℂ heißt P s - zulässig, wenn G(X) = ∑ Y ≥Xg(Y )Ps(Y ) für alle X ∈ ℕs konvergiert und lim x→x∞G(X) = 0, also die Folge der Partialsummen konvergiert.
Wir definieren nun eine Ableitung von G(X) nach Ps:
Definition. Ist G : ℕs → ℂ, dann sei
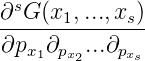
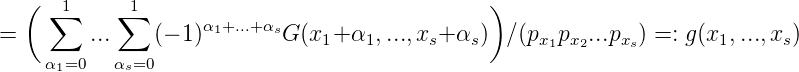
für (px1px2...pxs) > 0
Also ist g(x1,...,xs) fast überall definiert. Wir beweisen nun den
Beweis. O.B.d.A. sei G(X∞) = 0, also G ∈ C0(B) bzw. ∈ C0(ℕ∞). Es ist dann
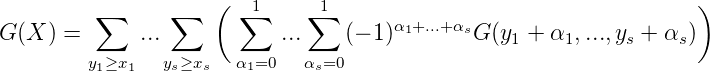
Wir betrachten nun nach kurzer Rechnung für
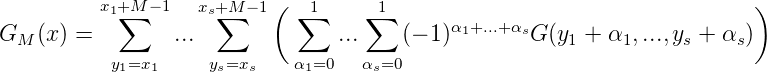
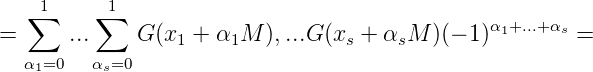
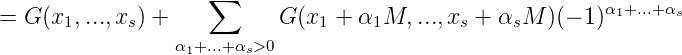
In sedem der 2s - 1 Summanden ist mindestens ein α i = 1. Da für M → ∞ also (x1 + α1M,...,xs + αsM) → X∞ geht und G(X∞) = 0, gilt lim M→∞GM(X) = G(X), was zu zeigen war. __
Eine Funktion g(X) ist genau dann Ps-integrierbar, wenn |g(X)| Ps-integrierbar ist:
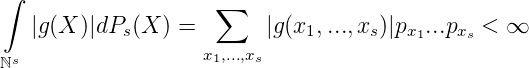
Die Reichendarstellung von G(X) ∈ C(ℕ0) ist sedoch i.A. nicht absolut konvergent. Wir schreiben diese wieder als Eichmaß-(Gauge-) Integral bezüglich Ps
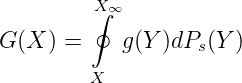
Wir definieren nun die Totalvariation einer Folge (Funktion) auf ℕs:
Definition. Ist G : ℕs → ℂ, dann ist die Totalvariation
V (G) = ∑
x1,...,xs ∑
i=01....∑
i=01(-1)α1+...+αsG(x
1 + α1,...,xs + αs)
∑
i=01....∑
i=01(-1)α1+...+αsG(x
1 + α1,...,xs + αs)
Es ergibt sich sofort, dass gilt
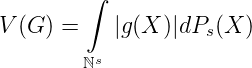
Analog ergibt sich der
Satz 10. Ist V (G) < ∞, so ist G(X) ∈ C(B). Wenn g(X) ∈ L1(B,Ps),L1(B,Ps) = {g(X) : ∫ ℕs|g(X)|dPs(X) < ∞}, dann ist g(X) Ps- zulässig.
Weiters ergibt sich der
Wir kommen nun zur Ps- Gleichverteilung in (ℕs,P s) :
Sei X1,X2,...,Xm,... eine endliche oder unendliche Folge in ℕs,X m ∈ ℕs und sei G ∈ C(ℕs), dann sei
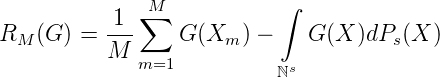
Sei nun V (G) < ∞, also ∑ X|g(X)|Ps(X) < ∞ und sei weiters χk1,...,ks(x1,...,xs) = 1 für 1 ≤ xi ≤ ki,i = 1,...,s, und = 0 sonst. Dann ist wie im eindimensionalen Fall
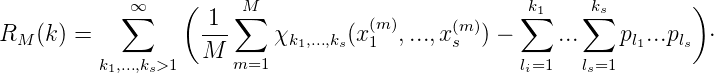
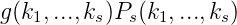
Definition. DM* = sup
(k1,...,ks)∈ℕs
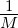 ∑
m=1Mχ
k1,...,ks(x1(m),...,x
s(m)) -
∑
l1=1k1...∑
ls=1ksP
s(l1,...,ls)
∑
m=1Mχ
k1,...,ks(x1(m),...,x
s(m)) -
∑
l1=1k1...∑
ls=1ksP
s(l1,...,ls)
Wir nennen in üblicher Weise DM* die *-Diskrepanz der X
1,....,XM
bezüglich des Maßes Ps.
Aus der Hölderschen Ungleichung folgt sofort der
Für die Einfachheit der Notation sei wieder l = (l1,...,ls) ≤ k = (k1,...,ks), wenn li ≤ ki für i = 1,...,s. Weiters sei Q(k) = {l : l ≤ k}
Definition. Für 1 ≤ p < ∞ seien die p- Diskrepanzen definiert als
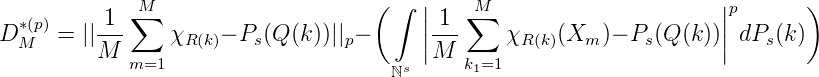
Aus der Hölder-Ungleichung, 1∕p + 1∕q = 1, folgt sofort der
Bemerkung: Nach dem Satz von James-Kakutani über reflexive Räume folgt für 1 ≤ p < ∞, dass es zu X1,...,XM seweils ein G mit V (q)(G) = 1 gibt, sodass |RM(G)| = DM*(p), sogar R M(G) = DM*(p), ist.
In Zusammenhang mit unserem Variationsbegriff sei an einen klassischen Satz von F. Riesz erinnert: F(x) sei genau dann als F(x) = C + ∫ 0xf(t)dt mit f(t) ∈ L p darstellbar, wenn für alle a = x0 < x1 < ... < xn = b gilt, dass es eine Konstante K > 0 gibt, sodass unabhängig von der Zerlegung von [a,b] gilt:
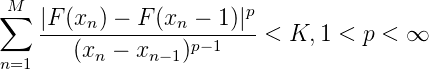
Bei uns ergibt sich zwanglos der analoge
Satz 14. G(X) = G(x1,...,xs) ist genau dann mit g(x1,...,xs) ∈ Lp als G(X) = C + ∫ y1≥x1...∫ ys≥xsg(y1,...,ys)dPs(Y ) darstellbar, wenn
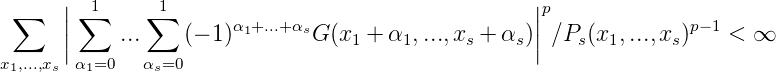
Wir kommen nun zur Ps-Gleichverteilung von Folgen (Xm)m aus ℕs bezüglich des Maßes Ps auf ℕs,P s(X) ≥ 0, ∑ XPs(X) = 1.
Definition. Die Folge (Xm) in ℕs ist P s glv., wenn für sedes X ∈ ℕs gilt: lim M→∞#{Xm = X, 1 ≤ m < M}∕M = Ps(X).
Es folgt sofort der
Satz 15. (Xm)m ist genau dann Ps- glv., wenn für alle G ∈ C(ℕs)
∞) gilt
lim M→∞
 ∑
m=1MG(X
m)
∑
m=1MG(X
m) ∕M -∫
ℕsG(X)dPs(X)
∕M -∫
ℕsG(X)dPs(X) = 0
= 0
Beweis. o.B.d.A., sei G(X∞) = 0. Sei K so groß, dass für max xi > K,X =
(x1,...,xs), gilt: |G(X)| < ϵ. Sei GK(X) = 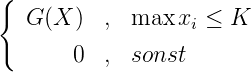
Dann ist
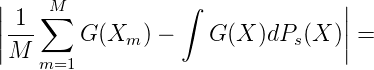
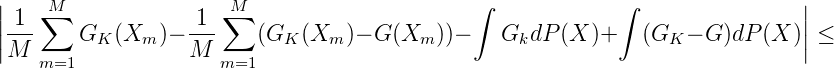
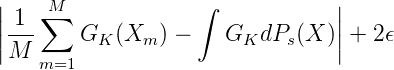
Sei M(ϵ) so groß, daß für max xi ≤ K gilt: für alle M > M(ϵ) ist
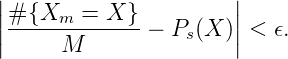
Dann ist für M > M(ϵ):

 ∑
m=1MG(X
m) -∫
GdPs(X)
∑
m=1MG(X
m) -∫
GdPs(X) < Ks. ||G||
n ⋅ ϵ + 2ϵ, w.z.z.w.
__
< Ks. ||G||
n ⋅ ϵ + 2ϵ, w.z.z.w.
__
Die Umkehrung ist trivial.
Definition. Wir bezeichnen nun mit DM(X) die lokale Diskrepanz an der Stelle X
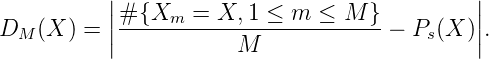
Offensichtlich ist (Xm)m Ps-glv., genau wenn DM(X) 0 ∀X.
0 ∀X.
Man zeigt in naheliegender Weise den
Wir übergehen den Beweis hier.
Sei Q ein Quader Q = [a1,b1] × .... × [as,bs] in ℕs. Dann sei
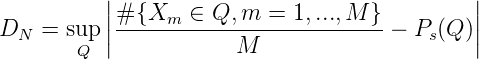
Es gilt offenbar DM* ≤ D M ≤ 2sD M* und D M(X) ≤ DM.
Die Größe ΔM := sup XDM(X) findet wie folgt Interesse:
Zunächst gilt ΔM ≤ DM ≤ 2sD M* in ((ℕs) ∞,Ps).
ΔM ist in folgendem Sinne eine Invariante:
Ist E abzählbar und diskret topologisiert, so sei h : E → ℕ bisektiv. h ist dann ein Homöomorphismus. Seien E∞ und ℕ∞ die Einpunkt-Kompaktifizierungen, dann ist die Ausdehnung von h auf E∞ → ℕ∞ ebenfalls ein Homöomorphismus. Wir übertragen nun das Maß P, P(E∞) = 1, auf ℕ∞ : π(h(X)) = P(X). Die Folge (Xm)m wird durch h bisektiv auf die Folge nm = h(Xm) abgebildet. Offenbar ist die lokale Diskrepanz ΔME der Folge (X m)m gleich der lokalen Diskrepanz ΔM NderFolge(n˙m)˙mbezüglichPbzw.π. Die lokale Diskrepanz ist also in diesem Sinn eine Invariante gegenüber von Bisektionen der abzählbaren Grundmenge. Das bedeutet, daß auf ℕs beliebige Maße zugelassen sind, sedoch die Totalvariation einer Funktion und DM* abhängig von der Anordnung der Punkte sind, welche durch h bestimmt sind.
Als weitere Folgerung ergibt sich der
Satz 17. Ausgestattet seweils mit der uniformen Norm ||G||n = sup X|G(X)| sind die Räume C(E∞) und C(ℕ∞) bzw. C0(E∞) und C0(ℕ∞) linear isometrisch. Weiters gilt für die Dualräume (C(E∞))′≃ (C(ℕ∞))′≃ l1(ℕ). Der Satz gilt sinngemäß auch für Banachraumwertige G : E∞ → R, R Banachraum.
Wir beweisen nun noch einen Satz vom Helly’schen Typ.
Sei (Gm(⋅))m eine Folge komplexwertiger Funktionen. Gm : (ℕs) ∞ → ℂ, sodaß ||Gm(X)||u ≤ K,V (Gm) ≤ K für m = 1, 2,.... Dann gibt es eine vage gegen eine Funktionen G konvergierende Teilfolge, sodaß ||G||u ≤ K und V (G) ≤ K.
Beweis. Wir zerlegen Gm(X) in Realteil und Imaginärteil und diese in positiven und negativen Teil:
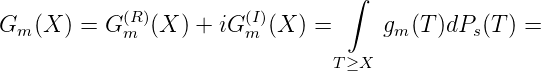
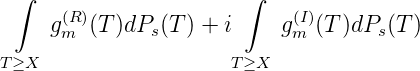
wobei die g fast überall definiert sind. Es ist
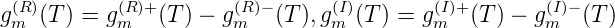
Die Funktionen
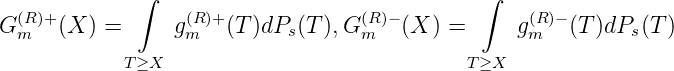
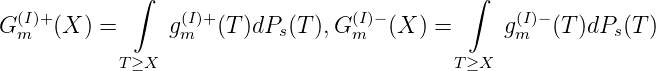
sind in ||⋅||n und V (⋅) durch K beschränkt und monoton fallend gegen Null. Nach dem Satz von Tichonow hat Gm(R)+(⋅) einen vagen Häufungspunkt.
Sei Gm1(R)+(⋅) eine Teilfolge, die für alle X gegen eine Funktion G(R)+(X) konvergiert, ||G(R)+|| u ≤ K, V (G(R)+) < ∞. Die Folge G m1(R)- hat ebenso eine Teilfolge, die gegen ein G(R)-(X) = lim m2→∞Gm2(R)-(X) konvergiert, wobei ||G(R)-|| u ≤ K, V (G(R)-) < ∞. Analog gibt es Teilfolgen (m 3)m3 von (m2)m2 und (m4)m4 von (m3)m3, sodaß es Funktionen gibt mit
lim m3→∞Gm3(I)+(X) = G(I)+(X), lim m4→∞Gm4(I)-(X) = G(I)-(X),∀X, die durch K normbeschränkt sind und von endlicher Variation sind. Dann gilt für alle X
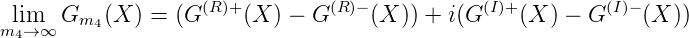
Sei wieder m = mn gesetzt. Wegen
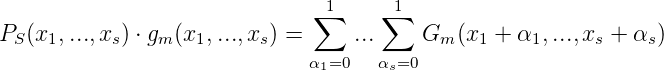
und wegen lim Gm(X) = G(X) = G(x1,...,xs) gilt für fast alle X
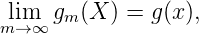
wobei gilt
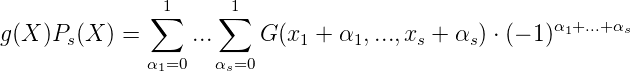
Folglich gilt lim |gm(X)| = |g(X)| Ps-fast überall.
Laut Voraussetzung ist für alle m = 1, 2,...
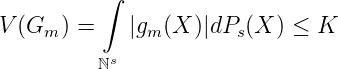
nach dem Lemma von Fatou gilt somit
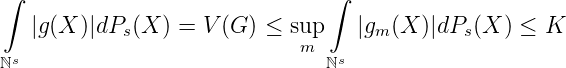
Da laut Konstruktion auch ||G||u ≤ K ist, ist der Satz bewiesen.
Wir stellen nun skizzenhaft eine Brücke zu den Kettenbrüchen her, wobei wir aus Platzgründen die Beweise knapp halten müssen.
Sei I = (0, 1),I = [0, 1], und für t ∈ (0, 1), sei T definiert durch
1∕t = ⌊1∕t⌋ + {1∕t} = ⌊1∕t⌋ + Tt; dann ist die Kettenbruchentwicklung von
t = [a1,a2,...,an + Tnt], welche genau für rationale t abbricht: t = [a
1,...,an] mit
an ≥ 2, da 0 ≤ Tnt < 1. Sei u = (w
1,w2,...) ∈ ℕ∞ℕ beliebig. Wir identifizieren die
rationalen t ∈ (0, 1) mit der Klasse von Folgen 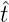 = (a1,a2,...,an,∞,u),u ∈ ℕ∞ℕ.
Ô := (∞,u),
= (a1,a2,...,an,∞,u),u ∈ ℕ∞ℕ.
Ô := (∞,u), 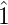 := (1,∞,u). E∞ := {
:= (1,∞,u). E∞ := {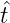 ,t ∈ [0, 1]}, wobei für t ∈I - Q gilt
,t ∈ [0, 1]}, wobei für t ∈I - Q gilt
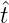 = (a1,a2,...,an,...),an ∈ ℕ, sodaß t ↔
= (a1,a2,...,an,...),an ∈ ℕ, sodaß t ↔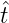 eine Bisektion I ↔ E∞ erzeugt. Wir
übertragen die natürliche Topologie von I nach E∞.
eine Bisektion I ↔ E∞ erzeugt. Wir
übertragen die natürliche Topologie von I nach E∞.
Wir bilden nun ℕ∞ℕ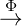 E∞ ab: Für X ∈ ℕ∞ℕ sei Φ(X) = X = (xn)n falls
xn < ∞ für n ∈ ℕ. Ist in X = (xn)n, x1,...,xn0 < ∞, xn0+1 = ∞, so sei
Φ(X) = (x1,...,xn0,∞,u). Φ ist bisektiv auf ℕ
N, Φ ist sursektiv ℕ∞ℕ → E∞ und stetig, da wir ℕ∞ mit der Einpunktkompaktifizierung
der diskreten Topologie von ℕ austatten.
E∞ ab: Für X ∈ ℕ∞ℕ sei Φ(X) = X = (xn)n falls
xn < ∞ für n ∈ ℕ. Ist in X = (xn)n, x1,...,xn0 < ∞, xn0+1 = ∞, so sei
Φ(X) = (x1,...,xn0,∞,u). Φ ist bisektiv auf ℕ
N, Φ ist sursektiv ℕ∞ℕ → E∞ und stetig, da wir ℕ∞ mit der Einpunktkompaktifizierung
der diskreten Topologie von ℕ austatten.
Wir statten nun diese Räume mit einem Maß aus: Sei P = (pn)n,pn ≥ 0,∑
pn = 1,p∞ = 0,
ein Wahrscheinlichkeitsmaß auf ℕ∞ und P∞ das Produktmaß auf ℕ∞ℕ. P∞ ist
borelsch, ℕ
NhadasvolleMaß;NˆNentsprichtI-Q.WirübertragenP˙∞ auf E∞ und auf
I,μ(A) := P∞(A).
Der Kettenbruch-Operator T ist auf E∞ und ℕ∞ℕ der einseitige Shift, also P∞- maßtreu, ergodisch, etc. Tn, n = 1, 2,..., ist dann μ-l.ü. definiert.
Sei S : ℕ∞ℕ →I definiert durch S(X) = [x1,x2,..., ], X ∈ ℕ∞ℕ, und sei F(t) := P∞(S(X) < t). Dann gilt der Satz
Satz 19. F(t) = ∑ n=1∞(-1)n-1(p tn-1,ptn-2 - pt1p0) ∑ h≥tnpk mit t = [t1,...,tn,..],p0 = 1. Die Reihe bricht für rationale t = [t1,...,tn]ab.
Es ergibt sich der weitere Satz
Ein Beispiel: Sei pn = p(1 - p)n-1 = pqn-1, n = 1, 2,..., die geometrische Verteilung. pn ist die Wahrscheinlichkeit, daß man genau n Bernoulli-Versuche braucht, um zum ersten Erfolg zu kommen. Die geometrische Verteilung ist wie die Exponentialverteilung gedächtnislos. Es ergibt sich
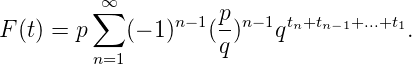
Für p = 1∕2 ist F(t) =?(t), die Minkowski’sche Fragezeichenfunktion, die bekanntlich stetig aber nicht absolut stetig ist. ?′(t) = 0 für t ∈ Q.
Allgemeiner: sei F(t) ↑ stetig. F(0) = 0,F(1) = 1,F(t) = τ,F : [0, 1] → [0, 1],t = F-1(τ),t 1,...,tM ∈ [0, 1],τ1 = F(t1),...,τM = F(tM)
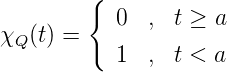
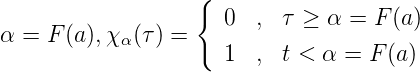
Sei G(t) : [0, 1] → ℂ,V (G) = sup x1≤x2≤...≤xN ∑ n=1MG(x n-1) - G(xn) < ∞. Sei
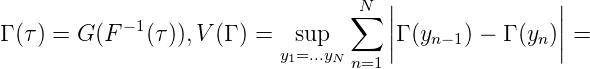
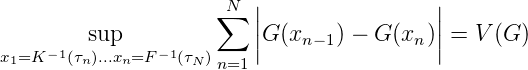
Sei λ das Lebesque-Maß und μ das durch F(t) erzeugte Maß auf [0, 1]. Sei τ1,...,τM ∈ [0, 1] xm = F-1(τ m),m = 1,...,M.
![|
D * (λ) = sup ||#-{τn <-α,m--=-1,...,M--}- λ([0,1]) =
M 0≤α<1 | M](4.4.21-Skript-2143x.png)
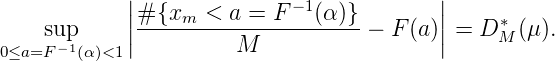
Satz 21. Ist F(t) ↑ stetig in [0, 1],F(0) = 0,F(1) = 1, und F(t) = τ ist G(t) : [0, 1] → ℂ, ist Γ(τ) = G(F-1(τ)), so ist V (G) = V (Γ). Ist t1,...,tM ∈ [0, 1],τ1 = F(t1),...,τM = F(tM), so ist
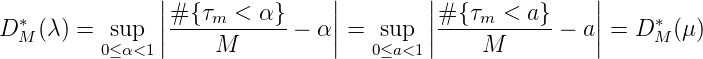
Wir können nun Gleichverteilung von Folgen und Diskrepanz bezüglich der Maße betrachten:
Sei F(t) ↑, stetig, F(0) = 0,F(1) = 1,F(t) = τ,t = F-1(τ). Seien t1,...,tM ∈ [0, 1],τ1 = F(t1),....,τM = F(tM). Seien χa(t) = 0 für t ≥ a,χa(t) = 1 für t < a, α = F(a),χα(τ) = 0 für τ ≥ α = F(a),χα(τ) = 1 für t < α = F(a).
Sei G(t) : [0, 1] → ℂ mit V (G) = sup x1≤x2≤...≤xN ∑
n=1∞ G(xn-1) - G(xn)
G(xn-1) - G(xn) < α
< α
Sei Γ(τ) = G(F-1(τ)), dann ist V (Γ) = sup
y1≤...≤yn ∑
n=1N Γ(yn-1)-Γ(yn)
Γ(yn-1)-Γ(yn) = V (G)
= V (G)
Sei λ das Lebesque-Maß und μ das durch F(t) = τ erzeugte Maß auf [0, 1]. Sind T1,...,TM ∈ [0, 1], xm = F-1(τ m),m = 1,...,M, dann gilt offenbar der
Satz 22. Ist F(t) ↑ und stetig, F(0) = 0,F(1) = 1,F(t) = τ und G(t) : [0, 1] → ℂ,V (G) < ∞, Γ(τ) = G(F-1(τ)), so ist V (k) = V (Γ). Sind τm = F(tm),m = 1,..,M, dann gilt
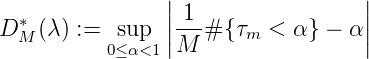
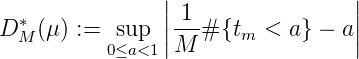
Bemerkung: Das Mengensystem {Ba = S-1([0,a)), 0 < a ≤ 1},B a ⊆ E∞, erzeugt die Diskrepanz
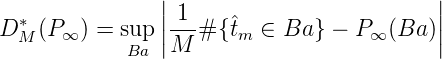
der Folge ( m)m aus E∞. Es gilt DM*(P
∞) = DM*(μ) = D
M*(λ) für seweils die
Folgen (
m)m aus E∞. Es gilt DM*(P
∞) = DM*(μ) = D
M*(λ) für seweils die
Folgen ( m), (tm)m, (τm)m.
m), (tm)m, (τm)m.
Spezielle Literaturangaben erscheinen nicht nötig, da alle verwendeten Begriffe und Sachverhalte im Internet rasch aufzufinden sind.